2年生に入ると一次関数に入ります。
比例のグラフの平行移動と考えれば良いわけですが、なかなかそう見れない子もいます。
手を動かして、その感覚を掴んで欲しいですね。
今回は、
切片は$y$軸の点、傾きは$x$が1増えると$y$が傾き分増えると
基本のかき方を習った後にやる活動を想定しています。
一次関数のかきかたの習熟をねらいます。
模様が出てくるので、子どもが美しいなと合わせて感じてもらえれば最高です。
1時間で完了する想定です。
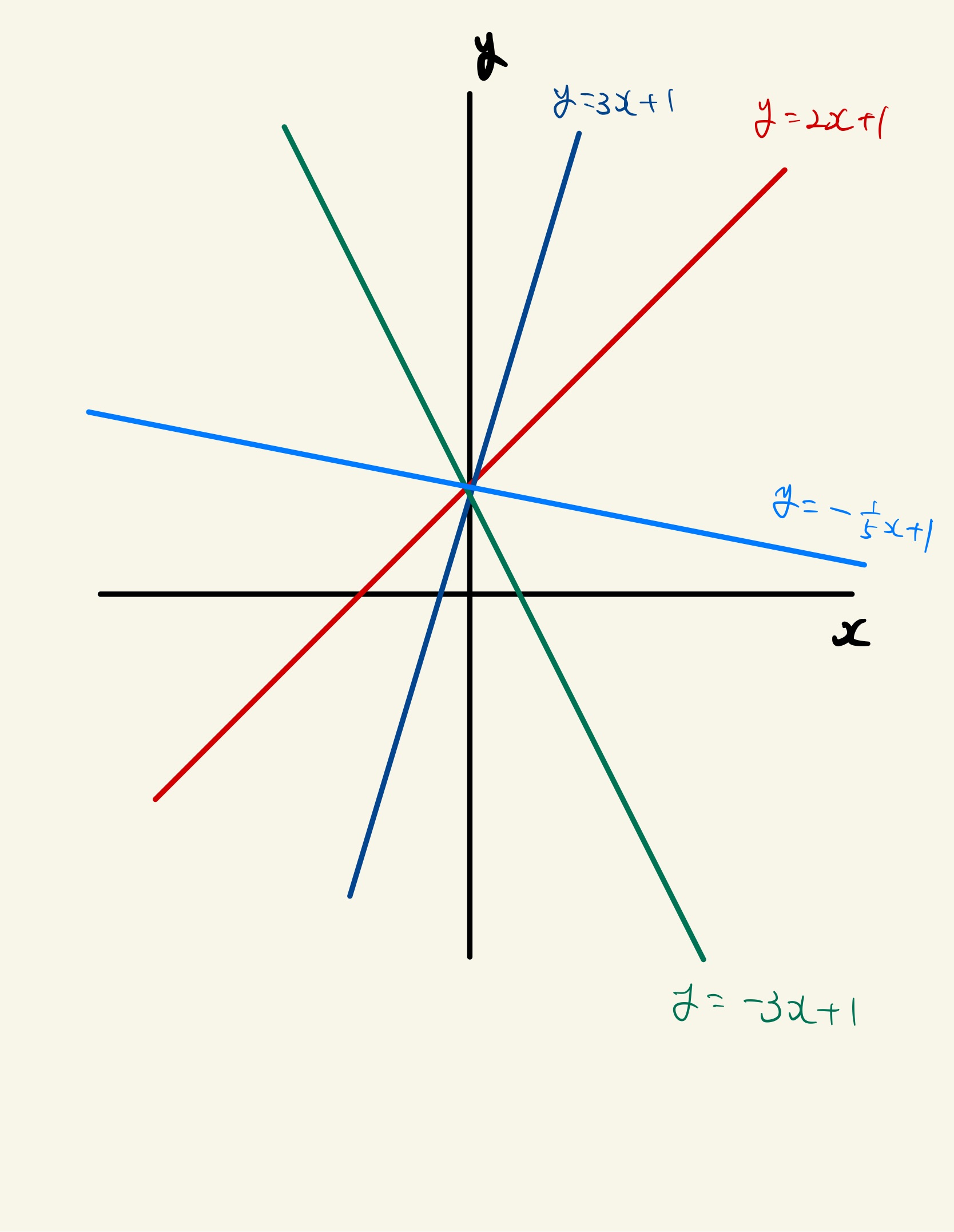
傾きを変えると・・・?
前時の問題を使って(今回は$y=2x+1$とします。)
「今日で一次関数のグラフをマスターするよ!
傾きの数字だけ色々変えて、グラフをかいてみよう。傾きの値を幾つする?」
と子どもに聞きます。
色んな値を入れますが、賢明なみなさんならもう頭で想像できますよね?
そうです。
切片を中心に放射状の模様が出来上がります。
別の記事で1年生でも同じ活動を提案しました。
以前に授業でやっているならば、覚えている子は比例と同じだと気づくでしょう。
切片を変えると?
こうすると次は切片の値を変えると模様が出てくるのかなと考え出すのは自然です。
子どもの疑問を取り上げたいですね。
もし、教師から促すのだったら
「切片の値を変えても同じ模様ができるのかな?」
と発問します。
そこで、少しストップして予想させます。
どんな模様がでると予想するでしょうか。
もちろん意見が出なかったらそのまま活動するで構いません。
でも、やる前に予想する。
ある見通しの元、確認・活動をするよさに気づいて欲しいと思っています。
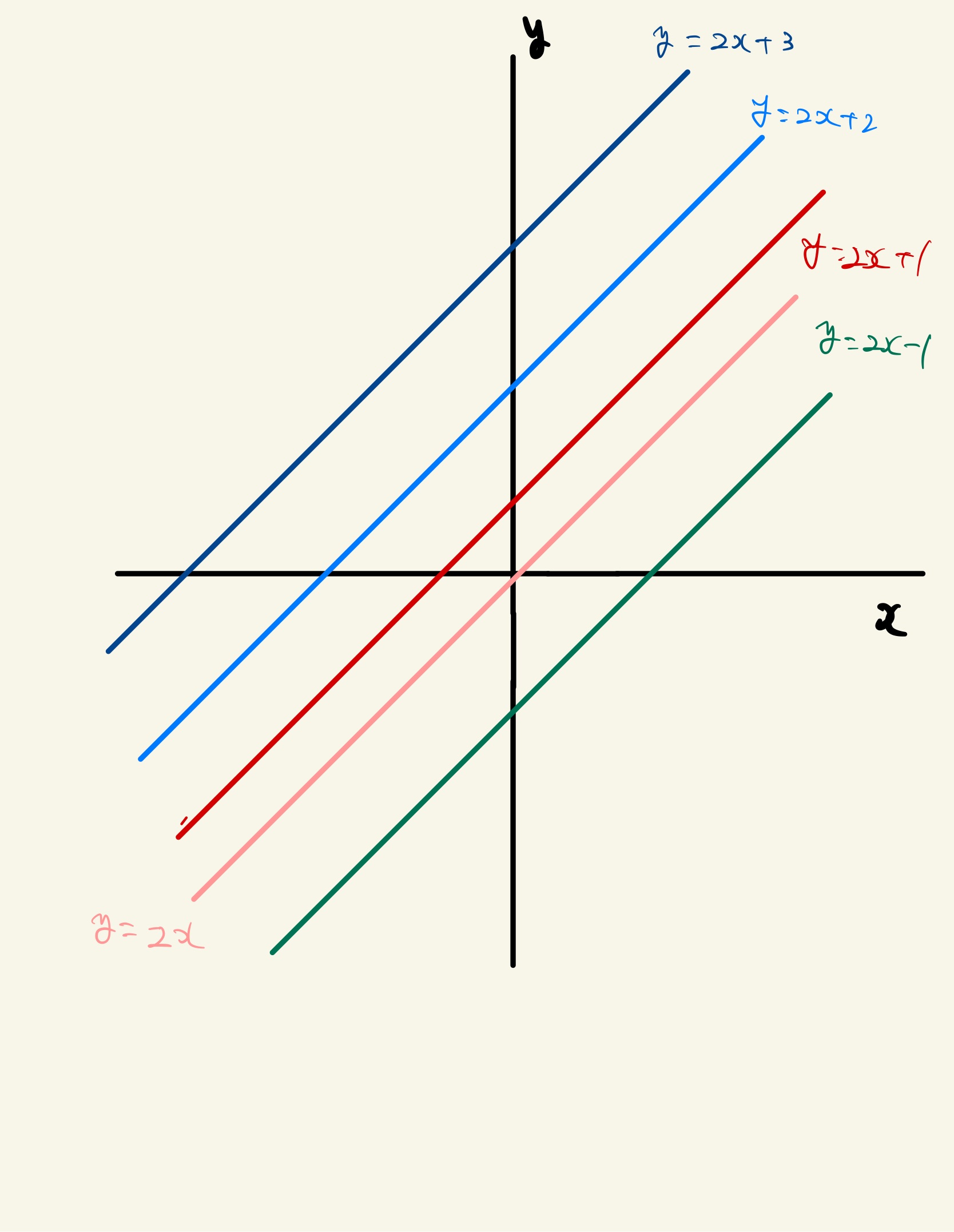
こんな感じになりますね。
これをみて、子どもはどんな発見をするでしょうか?
今後の授業との関わり(連立方程式と交点)
この後、連立方程式と一次関数の授業を行います。
2本の直線の関係は、
・一致する
・1点で交わる
・平行である
のどれかです。
今回は、「1点(切片)で交わる」、「平行である」場合を暗に取り上げています。
次の時間に連立方程式を計算して交点を求めていきます。
計算で終わってしまいがちですが、何とかしてグラフと計算の橋渡しをしたいですね。
まとめ
今回は、一次関数のグラフの習熟を少しでも楽しくすることを念頭にした授業です。
そしてこの授業は布石で、連立方程式と交点の話につなげます。
2つの関数の式を見て、どんなグラフかピンとくる子どもを育てたいですね。
【こんな一次関数の授業も行いました】
⇓その授業はこちら!⇓








コメント