一次関数の導入では、よく「最初から何センチか水の入っている水槽に、水を入れていく。そのときに経過時間を$x$(分)、水の高さを$y$(cm)として、表に表したり、グラフに表す」ことを行います。
そのあと、一次関数のグラフをかけるようにしたり、グラフから式を求められるようにしたりします。
そして、方程式の解をグラフに表していくことで、2つのグラフの交点から連立方程式の解を求めたり、$x=a$や$y=b$、$ax+by=c$の方程式をグラフにあらすとどんなことがわかったりするかを考えていきます。
方程式として$x=a$や$y=b$として、グラフに表せることも大切なのですが、生活場面で$x=a$や$y=b$のグラフを導入できないかなと考えて授業を作りました。
ねらい
水槽に水が貯まる場面を通して、変域や、$y=b$のグラフを理解できる。
(ホントは1兎を追うべきですが、2兎追います。)
問題
底から3cm分、水が入った水槽があります。
1秒間に水の高さが2cmずつ高くなるように、水槽に水を入れていきます。
この水槽の高さは9cmです。
水を入れ始めてからの時間を$x$(秒)、水槽の水の高さを$y$(cm)としたときのグラフを書きなさい
生徒の様子
生徒は、「なんだ$y=2x+3$のグラフを書けばいいんだね。」と意気揚々とグラフをかいていきました(下記参照)。
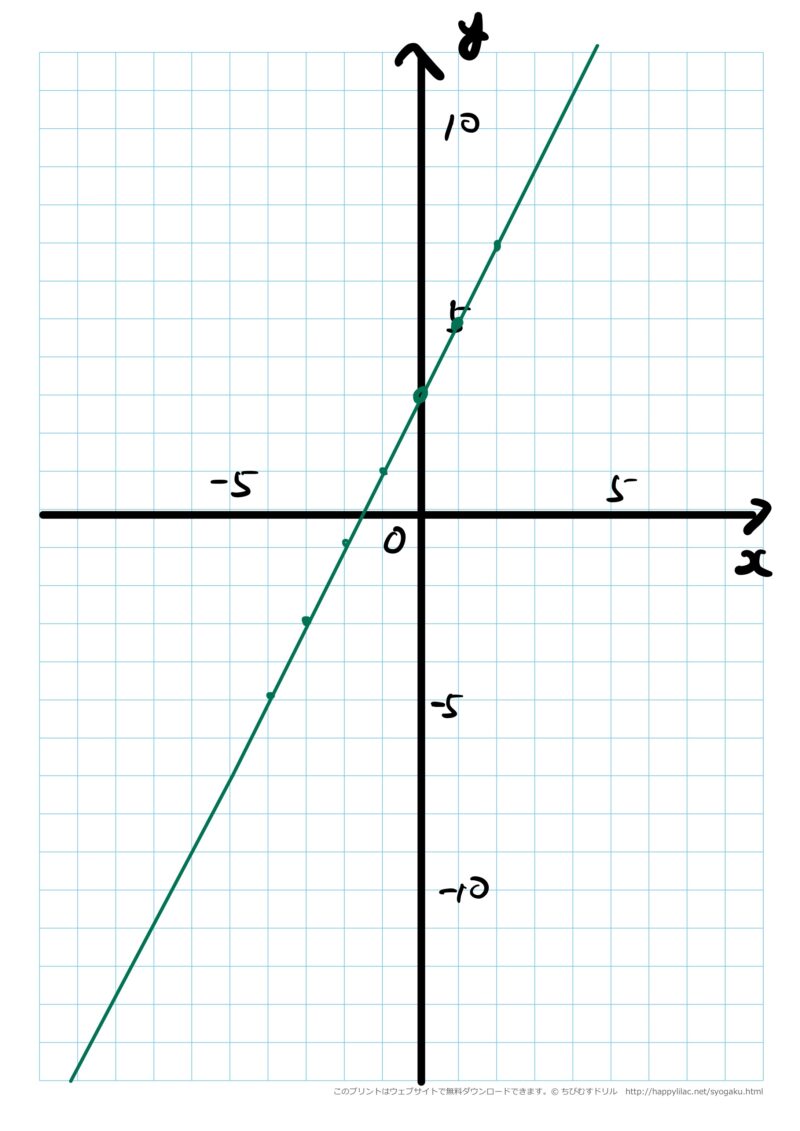
グラフをかくと、何人かの生徒が首を捻ります。
「これ、水槽の高さが9cmだから、3秒経ったら、水槽から水があふれるよな…。グラフの線をかいちゃいけないのかな。んー???」
そこで、こんな意見や、途中までしかグラフをかいていない生徒をとりあげ、グラフを全体に提示します。
「この子は、途中までしかグラフをかいていないけれど、どうして途中までしか書かなかったか、わかるかな?」
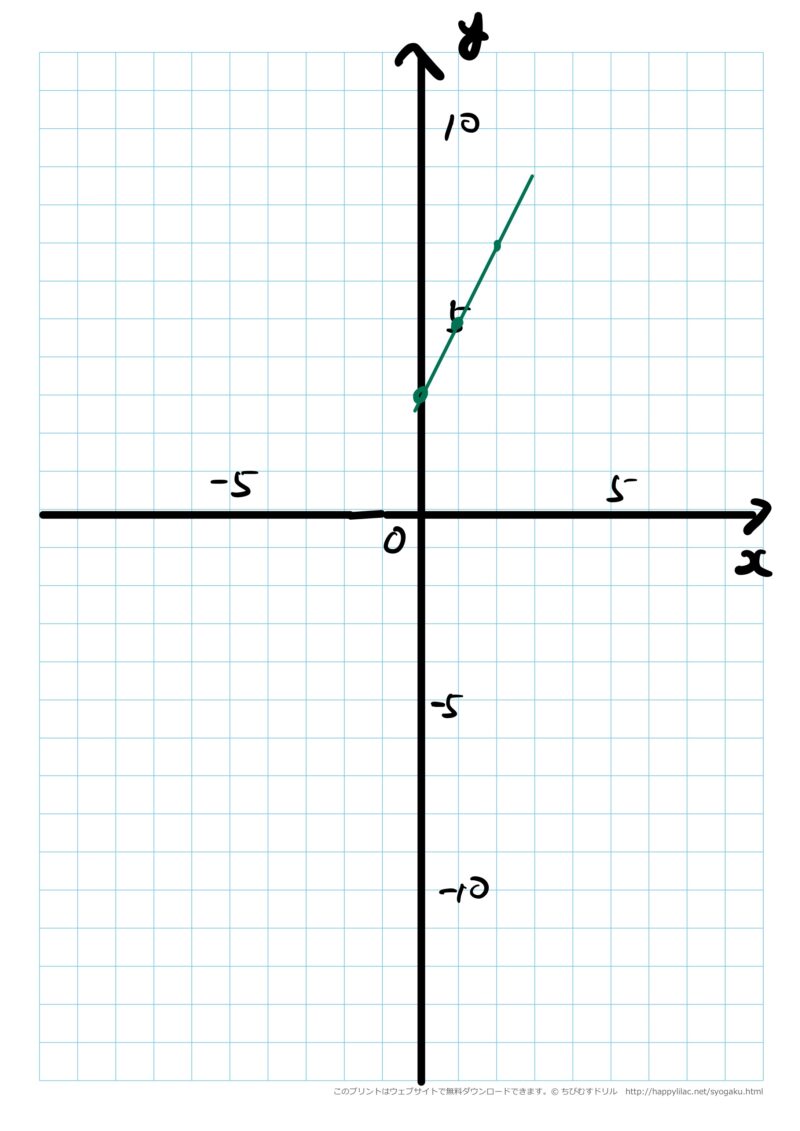
そうすると、「水槽の高さは、9cmだからそれ以上は水が溢れちゃうからグラフをかけない。$x<0$のときは、そもそも考えなくていいからやっぱりグラフはかかなくていいと思う。」という声が出てきます。
そこで、変域の説明をします。
「このグラフは$y=2x+3$のグラフだけれど、0秒から、3秒までしかグラフが書けませんね。書かない部分は、全く書かないか、点線で表現をします。」
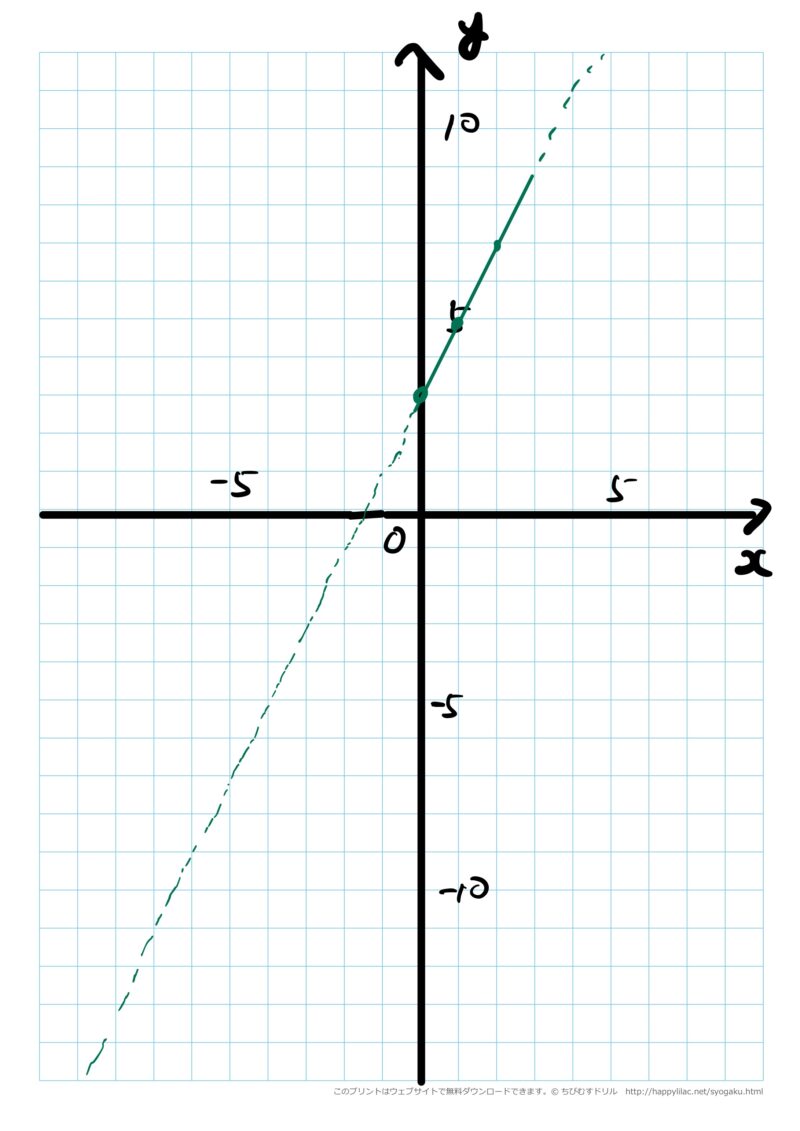
「0秒から、3秒までしかかかないから、$y=2x+3 (0 \leqq x \leqq 3)$とグラフの式を書いて、ここまでしかグラフをかかないよ、とわかるようにします。これを変域といいます。$y$の変域は…」
と、$y$の変域についても説明を加えます。
さらに「さっきの子は、3秒でグラフをかくのをやめたけれど、3秒後のグラフをかいた子もいるよ。どんなグラフになるかわかる?」
と聞いて次のようなグラフを提示します。
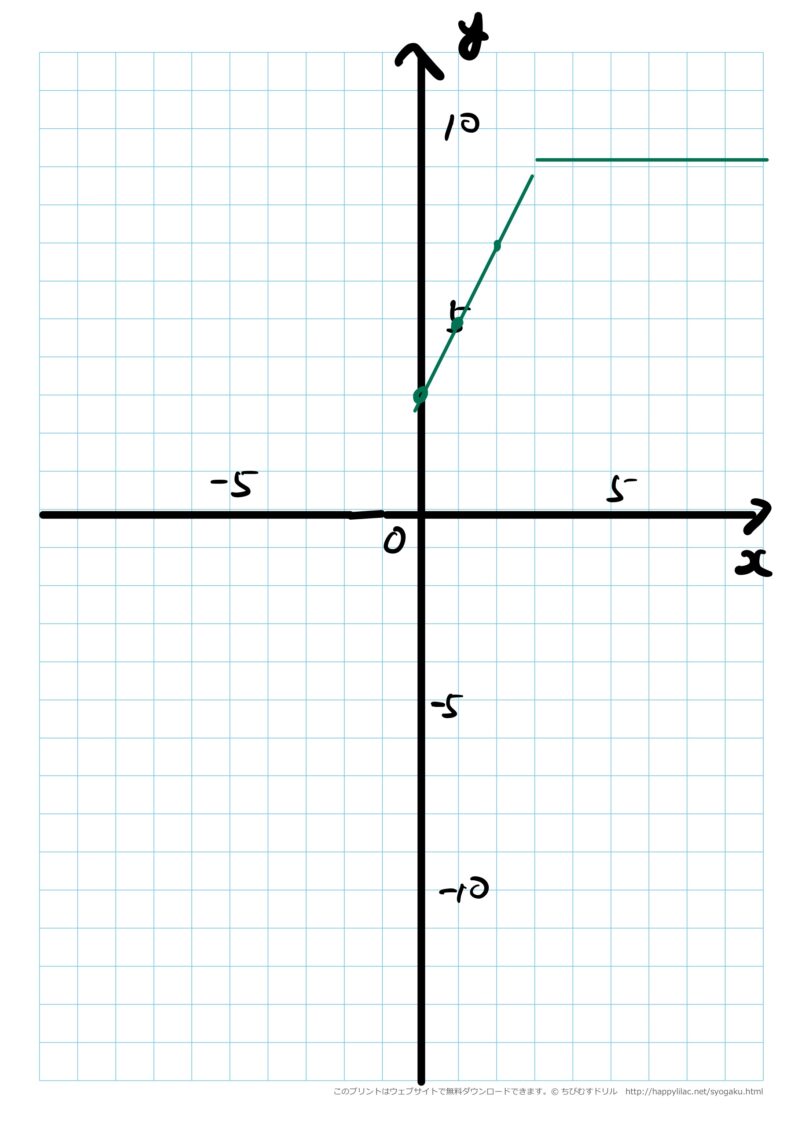
生徒は、「水槽の水があふれるもんで、高さは変わらないよね。どこにも水を止めるなんて書いてないもんね。」と納得をします。
そこで、「じゃぁ、この横ばいになっているときのグラフの式はどう表現するといいのかな?」と問い返します。
生徒からは「ずっと、(水の高さの)$y$が9cm」という言葉が出るので、
「○○さんが言ったように、ずっと高さ、つまり$y$が9だから、$y=9$と表します。」
と教えました。
最後に
「今までの関数の定義って覚えてる?$x$の値が決まると、$y$の値がただ一つに決まるものを関数っていったよね。今回$y=9$って、$x$が出てきていないじゃない。これは関数ではないね。
次回からは、関数ではないグラフについて勉強をしていくよ」
ということで、$x=a$や$y=b$、$ax+by=c$といった方程式のグラフについて勉強をしていくことを伝えます。
まとめ
現実世界の事象でグラフを考えることで、変域が必要であることや、グラフが横ばいになる場合があることを生徒に気づかせることはできたと思います。
中学校数学で難しいのは、だんだん抽象的になってきて、実生活と乖離していくことだと思います。
すべてが全てとは言いませんが、折に触れて、実生活との関連を感じられるような教材を用意したいですね。

【他の一次関数の指導案はこちら】






コメント