直方体(立体)の対角線を求める以下のような典型問題がどの教科書でも紹介されています。
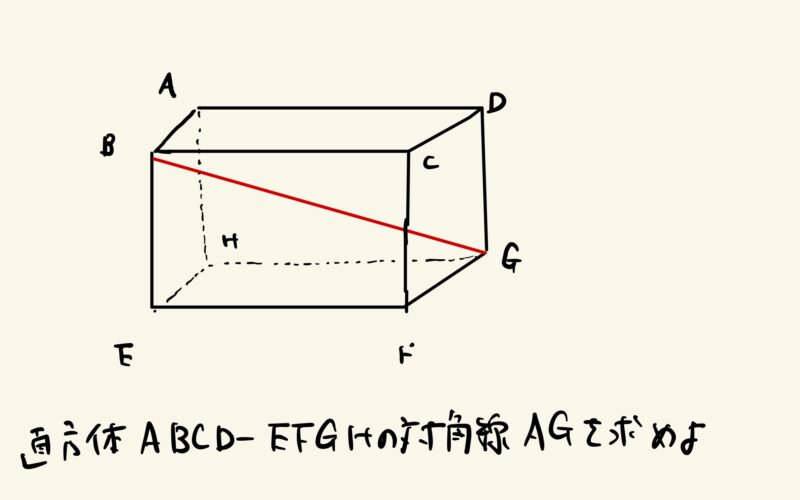
皆さんはどのように解かれますか?
教科書に載っている内容
教科書や、インターネットでいくつか調べてみましたが、以下のような解き方ばかりでした。
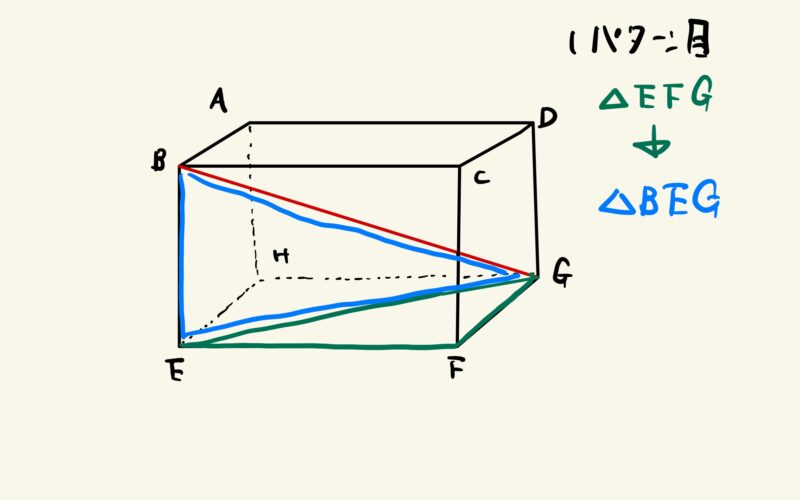
直角三角形が見えやすいですし、この解き方が1番オーソドックスです。
解き方は以下のようになります。
解答
△EFGで三平方の定理を使って
$$EF^2+FG^2=EG^2・・・①$$
△BEGで三平方の定理を使って
$$BE^2+EG^2=BG^2$$
①を代入して
$$BE^2+EF^2+FG^2=BG^2$$
$BG>0$なので
$$BG=\sqrt{BE^2+EF^2+FG^2}$$
というのをみて、三平方の定理が拡張された感じ!ってなります。
でも、この授業において、子どもにつけたい数学的見方ってこれだけなんでしょうか?
注目する直角三角形の組は一つじゃない!
僕がこの授業で大切にしたいことは、
「他にも対角線を求められる直角三角形は他にもある」ということです。
あと2組存在します。
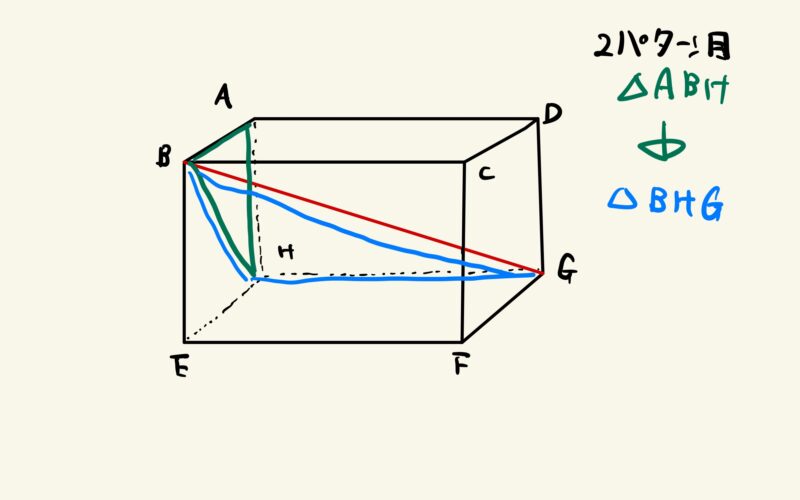
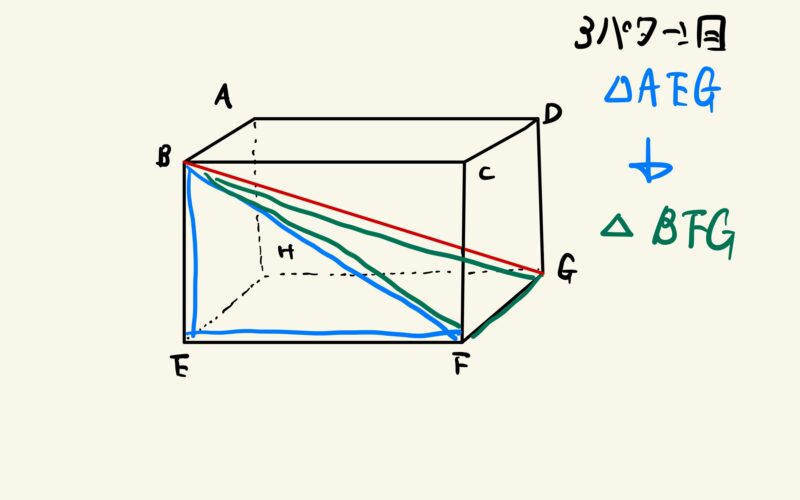
数学で大切なことの一つに、いろんな解き方で同じ結論に達することで、その解答がさらに強固なものになるという考えがあります。
一つの解法をみんなで納得した後、「他にも解き方あるかな?」とぜひ問い返したいものです。
余談ですが、京都大学の受験生が、数学の問題に対して、他の問題は全く解けなかったが、一つの問題に対して、複数の解答を書き提出したところ、数学のテストの点数が満点で返ってきた。
なんて逸話もあります。
京大がどんな学生を求めているか分かる逸話ですね。
もし1人で、何パターンも解放を見つけることができたらベタ褒めしたいですね。
まとめ
今回は、数学を使って、早く簡単に解けるという方法ではなく、一つの問題を多面的にみるということをテーマに授業を考えています。
どちらも大切です。
授業者としては、それぞれの授業で何をテーマに勉強していくかを考えながら授業を構成したいですね。





コメント