中学校1年生 比例の学習の肝は
「負の世界への拡張」
です。
負の値を習ったことで比例定数が負の値を取れるようになります。
そうすると$x$軸、$y$軸が負の値まで拡張されます。
学習の順序としては、比例定数は正の値のままで、$x$がを負の値をとると・・・と、座標軸を拡張していきます。
二次関数の時も書きましたが、グラフをかくなかで、綺麗だな、規則性がありそうだな。
そんな数学的見方を引き出したいですね。
今日はその最序盤の授業展開について書いていきます。
想定は2~3時間です。
まずは復習
大きな水槽に毎分2センチずつ水を入れます。経過した時間を$x$軸、水面の高さを$y$軸として、グラフに表しなさい。
という問題で導入が好きです。
連続量になることと、絵に表しやすいからです。
そこで、絵を描きながら、小学校のグラフを総復習していきます。
いちばん大切なのは表に表すことです。

そして、$y=2x$という式で表せること。
ここで、$x$の値を$y=2x$に代入すること。
$x$が1増えると、$y$が2増えることをきちんと抑えます。
$x$を代入すると、$y$の値が出ることが大切です。
負の世界への拡張
次は今書いた表に$x$が、負の場合を付け足していきます。
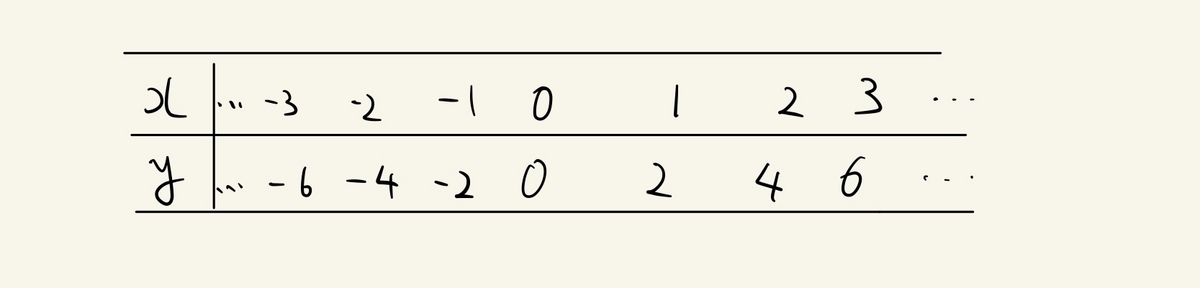
そして
「今から問題から離れて、数字だけで遊んでいくよ。水槽の話はちょっと忘れてね。
もし、$x$が負の数字を取れるようになったら、$y$の値はどうなるんだろうか?」
と尋ねます。
子どものなかで混乱する子がいると思います。
だって、$x$が0より前なら、水槽に水は入っていないので、$y$も0ではないかと考えるからです。
啓林館の教科書では、それを避けるために水を入れ始めてから、ある程度たった時間を$x=0$
とみなして問題を出しています。
ただ、これはこれでその場面状況を理解するまで時間がかかります。
負の数の世界になると、形式的な側面が増えてきます。
逆に慣れさせるチャンスと思って、水槽は置いておいて、話を進めます。
そうすると、
$x$が1増えると、$y$が2増えることは抑えてあるので、
$x$が1減ると・・・
と考え出します。
そうすれば、表は完成できます。
問題は、どのようにグラフに表すかです。
ここで、座標軸の書いてある黒板(ありますよね?)を取り出し、負の値まであるグラフを紹介します。
1つ、2つ、一緒に点を取って、残りは書かせましょう。
できる子は、
「さっきかいた線の延長じゃん」
と気づきます。
この気づきを取りあげ全体に広めましょう。
自分たちで比例定数を決めよう
さて、ここまで来たら、子どもに比例定数を決めさせて、もう2つ3つ、習熟のためにグラフをかかせます。
私が授業した時は、$a=1,2,5$が出てきました。
グラフをかくと次のようになります。

ここで、
「何か気づいたことはありますか?」
と考えさせます。
引き出したい気づきは4つです。
2.$y=5x$より急な直線は引けないかな
3.比例のグラフは必ず原点を通る
4.グラフの左上と右下(第2象限と第4象限)を通る直線はかけないのかな?
ここ辺りはきっと出てくると思いますし、出てこなかったら、数学的な見方をもっと鍛えたいものです。
2は直ぐに子どもたちは回答できます。
3もみんな同意するでしょう。
問題は1と、4です。
結構、1の気づきに対して、
「比例定数を負の値にすればよい」
という子どもは一定数います。
ピンチはチャンス。
実際に負の値の表とグラフをかかせて(比例定数も子どもに決めさせて)かかせると良いです。
分数という子ももちろんいるので、セットでかかせましょう。
比例定数が負の数をとると
先の章の話を納得したら、比例定数が負の数のグラフをかく練習をします。
ここはあえて教師が比例定数を指定します。
$a=−1,−2,−5$です。
私の意図分かりますか?

放射状の模様が出来ますよね。
そして、比例のグラフは「必ず原点を通る」ことにも気づかせることができます。
ちなみに(原点はなんでOなの?)
原点のOはoriginの略語です。
原初とか、起源という訳になります。
「グラフのど真ん中であり、負の数や正の数がここから伸びていくからoriginじゃないかな。」
と子どもに伝えて、定期テストに問題を出したところ、「原点」と書かずに「オリジン」とほとんどの子どもが書いてきました。
丸にしましたが、答案返却日後、徹底指導しました(苦笑)
まとめ
・比例定数が負の値を取り扱い、綺麗な模様作りをすると、子どもの印象に残る!
です。
感想を教えてください!
一次関数では、並行に模様作りをしていきます。(放射状の模様作りもしますが)
こちらをチェックしてください!
参考文献
結城浩(2019).「数学ガールの秘密ノート/学ぶための対話」.SBクリエイティブ







コメント