連立方程式を利用して、2本の直線の交点を求める学習があります。
教科書では、まずグラフをかいて交点を実際に求める方法を考えます。
その後、目で見て交点が分からない場合、連立方程式で計算で解いていく方法を考えます。
もちろん、計算で解けるのは大切ですが、もう一歩踏み込みたいなと考えます。
2つの直線の関係について、さらに踏み込んでみましょう。
⇓この授業の前時はこちら!⇓
教材研究
2本の直線の関係は
・1点で交わる
・平行である
・一致する
の3つです。
中学校の連立方程式で解く場合、解が求まる場合が、1点で交わる場合になります。
平行や、一致する場合の問題は取り上げられません。
グラフの感覚を豊かにする為にも、そこにも少し触れたいところです。
問題の提示(2直線が平行の関係)
次の問題を提示します。
2つの直線の交点を求めよ
$${\displaystyle \begin{eqnarray} \left\{\begin{array}{l} y = 2x+1 \\ y = 2x+3 \end{array} \right. \end{eqnarray}}$$
子どもはなんと反応するでしょうか。
前時では、連立方程式で解いています。
連立方程式で解いて、答えが出ないことに気づくでしょう。(両辺を差し引いて、整数だけ残る)
そこではじめて、グラフをかいてみようとなるわけです。
ただ、この2つの直線は前時で書いています。
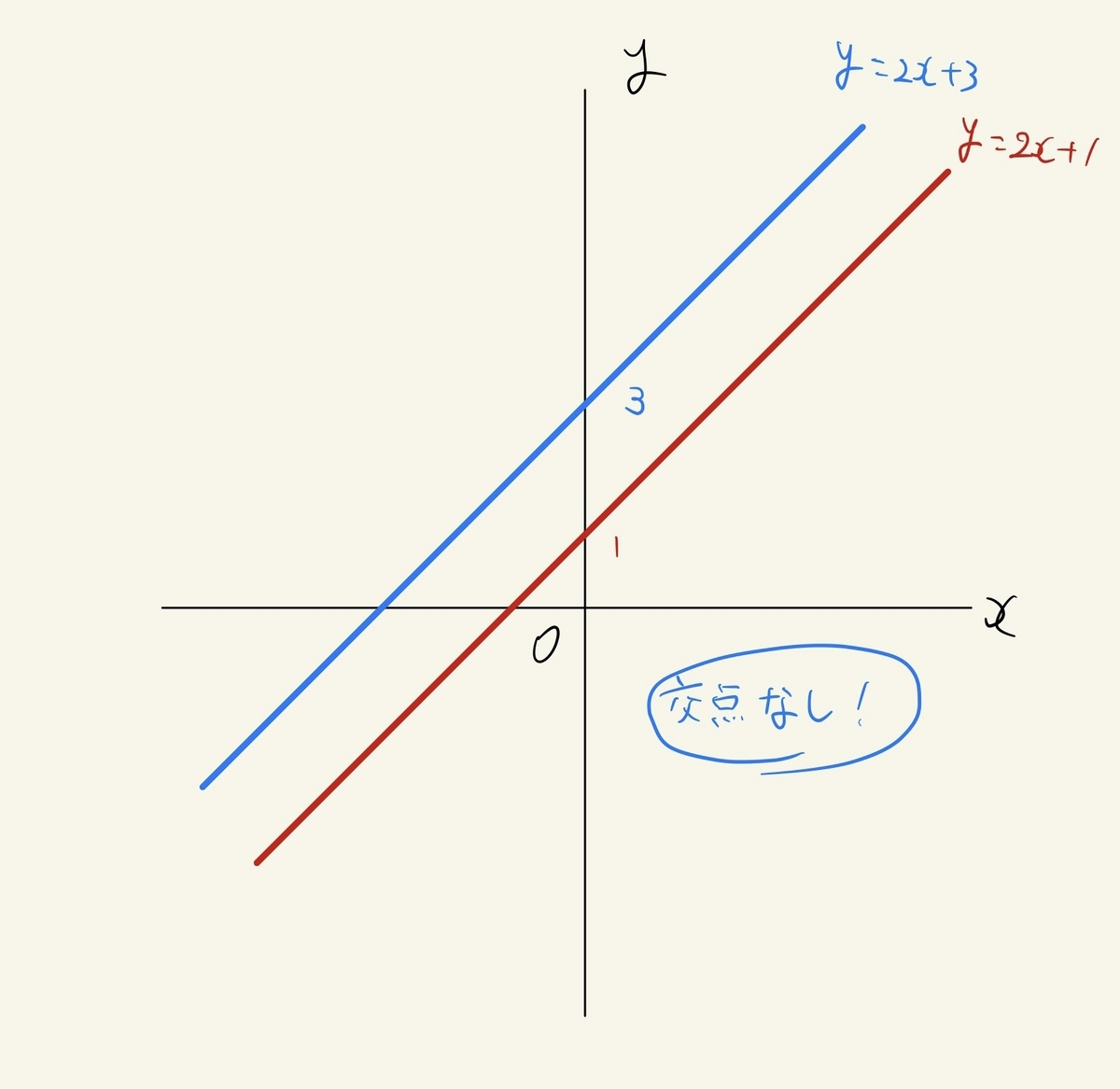
気づいた子はこのグラフの関係を見て、平行であることに気づき、交点を持たないことに気づくでしょう。
だから、解が存在しない(連立方程式を解けない・解は存在しない)ことに気づくのです。
さらに
「どうすれば平行と分かるのかな?」
と追加で発問して、傾きが等しいことに気づかせます。
そして、
「y=2x+1と平行なグラフの式を上げましょう」
と確認すると面白いです。
2直線が一致する場合
次の問題はこちらです。
$${\displaystyle \begin{eqnarray} \left\{\begin{array}{l} −2x+y = 1 \\ -4x+2y = 2 \end{array} \right. \end{eqnarray}}$$
これも連立方程式を解くことができません。
加減法で、2つの式を差し引くと、両辺が0になってしまいます。
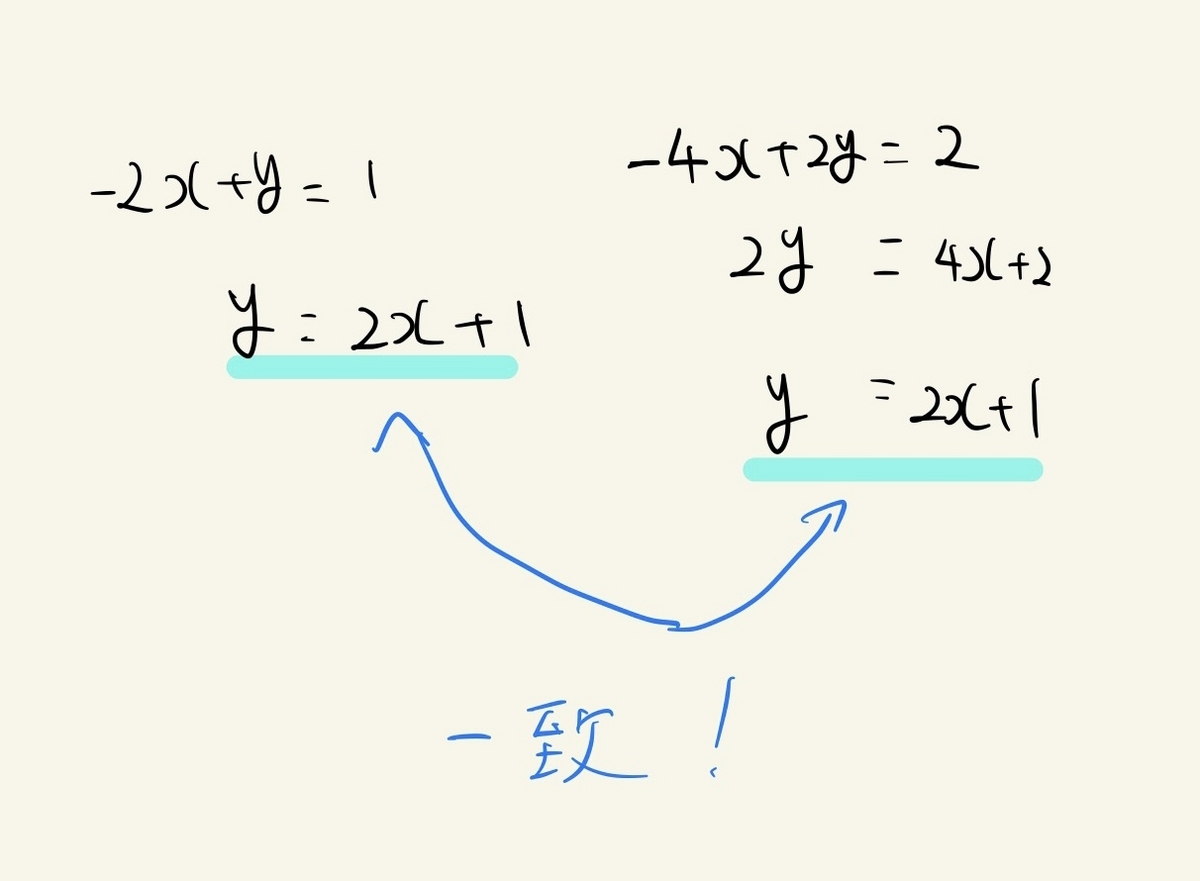
この場合は2つの直線はどうなるのでしょうか?
そうです。一致しますね。
これもグラフでかいて確認をした後、
「どんなときに2つの直線が一致するのかな?」
と尋ねれば、2つの式のどちらかを整数倍して、等しくなれば一致することに気づきます。
なんにしても、グラフと連立方程式の世界を何度と行き来し、橋渡しをしてくることが大切なのです。
最後に
「$y=2x+1$と一致する直線の式をあげましょう」
と、確認問題を出します。
まとめ
この授業は結構受けが良かったです。
必ず連立方程式は解が出るものと子どもは思っています。
しかし、解がでない。
これはなんで?
という場面に出会わせることで、連立方程式の有用性や関数との関係迫れます。

【他の一次関数の授業はこちら】






コメント