中学校3年生「平方根の利用」の問題です。
利用(文章題)になると、途端に子どもってひるみますね。
けれども、今回の問題はそんなことありません。
公式を忘れていても、果敢に問題に挑戦する姿が見られました。
問題
直径20cmの丸太から、切り口ができるだけ大きな正方形の角材を取る時、その切り口の正方形の1辺の長さは何cmになりますか?
啓林館.『未来へ広がる数学3』.p61より
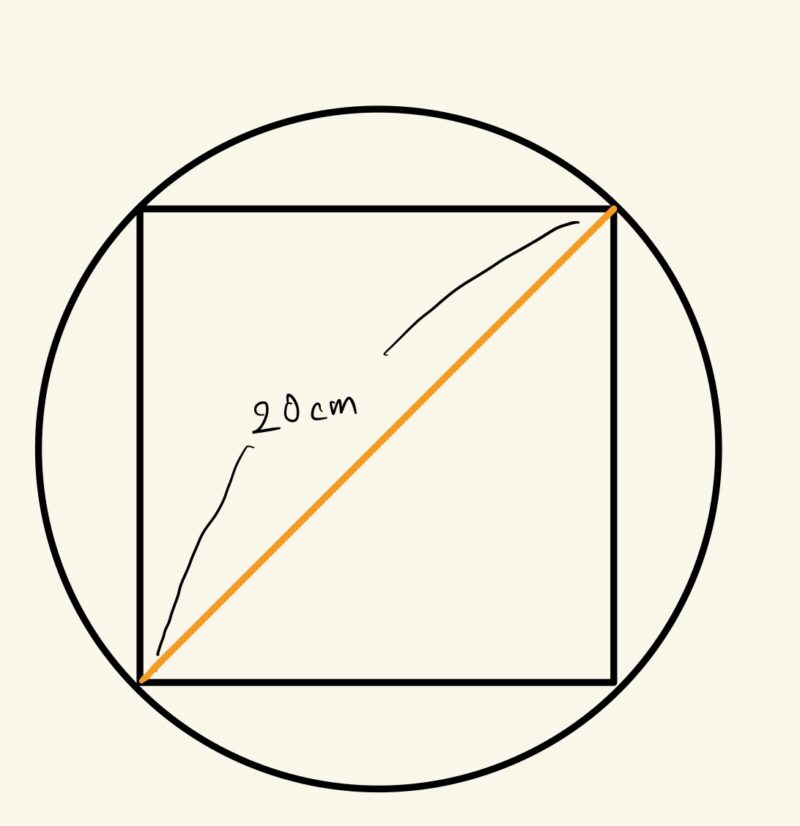
教科書でも紹介されている、一般的な解き方
正方形をひし形としてみれば、
$$(ひし形の面積)=(対角線)×(対角線)÷2$$
である。
これを使って、正方形の面積は、
$$20×20÷2=200$$
と求まる。
正方形の面積は、200㎠と分かったので、一辺の長さは$\sqrt{200}=10\sqrt{2}$となる。
$\sqrt{2}=1.414$として
$$10\sqrt{2}=10×1.414=14.14$$
と求めた。
これは一般的ですね。
実はこの問題、毎回「正方形をひし形として見て面積を求める。」しか方法はないと思っていました。
なので、ひし形の面積の公式を授業序盤に確認をして解かせるということが続いていました。
今年、ひし形の面積の公式を使わなくても解けるということを生徒が教えてくれました。
ひし形の面積の公式を使わない解法
式だけを書いてみます。
$$2(20×10÷2)=200…①$$
(後は先ほどの解答と一緒で)正方形の面積は、200㎠と分かったので、一辺の長さは$\sqrt{200}=10\sqrt{2}$となる。
$\sqrt{2}=1.414$として
$$10\sqrt{2}=10×1.414=14.14$$
①の式の見方
みなさん、①の式はどうやって計算したか分かりますか?
図に青線の補助線を引くと、
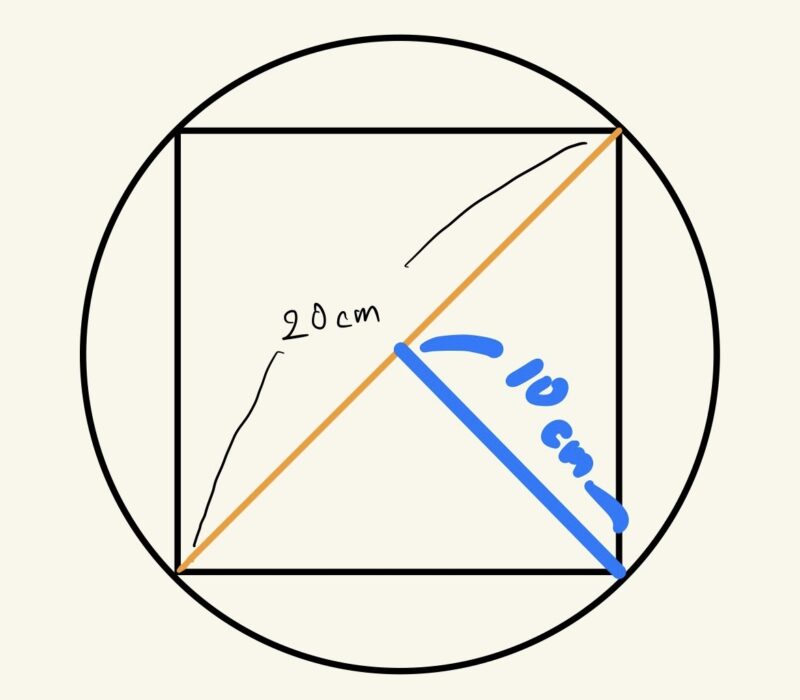
右下の直角三角形の面積が
$$20×10÷2$$
と出せます。
合同な直角三角形が2つあるので、
$$2(20×10÷2)=200$$
と正方形の面積が求まるんですね。
こっちの方が、公式を先に伝えなくても解けるし、汎用性が高い方法でした。
結局ひし形の面積の証明もこのようにやっていくんですよね(証明はひし形を対角線で四半分にしてやっていきますが)。
頭が固いなと気づかされました。
まとめ
生徒が気付かなければ公式を教えるのも一つの指導です。
けれども、公式を使わなくても解けるということを紹介することで、子どもも頭を柔らかくして解けるのではないでしょうか?
今回も子どもに気づかされた授業でした。
平方根の指導案







コメント