平方四辺形の導入の授業を紹介します。
定義・性質は、小学校でもやっているので、子どもたちは覚えていると思うのですが、もう一度振り返らせたい所です。
子どもが手を動かし、主体的に学ぶように、教材用意しました。
教材
平行四辺形導入授業の流れ
作図をしよう
子どもは、1番、2番は比較的かくことができます。
ただし、1番は三角定規の置き方は結構苦戦している生徒もいました。
生徒の様子を見て、三角定規の置き方をみんなで確認しながら復習すると、今後の数学に役立ちそうです。
また、2番についても、辺ABの長さだけを取って、コンパスで交点を作った結果、いびつな平行四辺形?ができている生徒もいました。
コンパスで同じ長さを取るというのがなかなかつかめない生徒も多くいます。
作図についてもう一度復習する、よいチャンスになります。

3つめの分度器を使っての作図については、2つ出てきました。
- 向かい合う角が180度になることを使って
- 平行の性質を使って
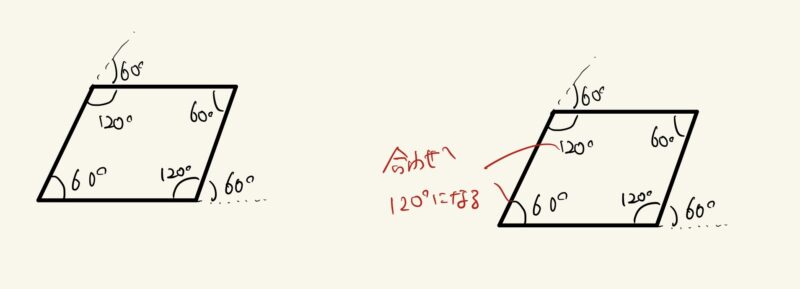
どちらも丸にしました。
定義と性質を確認しよう
3つの書き方を確認した後、平行四辺形の定義と性質を説明しました。
1番は平行四辺形の定義「2組の向かい合う辺が、それぞれ平行四角形を平行四辺形という」
2番は平行四辺形の性質①「平行四辺形の2組の向かい合う辺はそれぞれ等しい」
3番は平行四辺形の性質②「平行四辺形の2組の向かい合う角はそれぞれ等しい」
ということを使って作図をしたことを確認しました。
そして、定義を基に性質①,②の証明に入っていきました。
これはのちに勉強する「平行四辺形になるための条件」とかぶる所がありますが、このような流れを採用しました。
反省点
子どもは作図のところは活発に活動できました。
ただ、定義と性質をおさえるところで、「作図できるのに、定義と性質…??」と必要条件、十分条件が混乱していました。
しっかり教師がでて説明したつもりでしたが、上手くいかず。
来年への課題です。
まとめ
今回は作図から平行四辺形の導入を行ってみました。
生徒はよく活動し、知らず知らずのうちに平行四辺形の性質をつかっていきます。
そこを先生が捉え直して、生徒に返すことで、平行四辺形の性質がつかめます。
ぜひ授業をしたら感想を教えてください。







コメント