今回は、1年生の方程式の単元です。
方程式は、等式の性質を理解した後、移項を学び、機械的に解けるようにしていきます。
その中で、解法の逆のプロセスをたどることで、解法の理解がより深まるのではないかと考えました。
今回はその実践の紹介です。
みなさんの声をいただけたら幸いです。
参考にした本はこちら!
単元名と実践学年
方程式って何を表しているの? ―第1学年 「方程式」―
単元の目標
- 方程式の必要性と意味及び方程式の中の文字や解の意味を理解することができる。(知識及び技能)
- 等式の性質を基に、方程式を解く方法を考え、表すことができる。(思考力・判断力・表現力等)
- 方程式の良さに気づき、今までの解決過程を振り返って、考えることができる。(学びに向かう力、人間性等)
本時の目標
- 等式の性質を使って、解が3になる ax+b=cの形の方程式を作ることができる。
指導過程
(1)3x=6と、2x+3=9の違いは何か考え、課題を明らかにしよう
前時までに、等式の性質を使って簡単な一次式の方程式を解けるようになっている。
本時は最初にx=3、2x=6、2x+3=9の3つの方程式を提示し、解が3の方程式はどれか尋ねた【資料1】。
生徒達は、x=3をそれぞれの方程式に代入することを思い出し、3つの方程式全ての解が3になることを確認した。
次に、「解が分かっているから解けたけど、分かっていなかったら2x+3=9はどう解けばよいのか。」と尋ねた。
生徒達は困ったので、「3x=6と、2x+3=9の違いは何か。」と発問した。
そのときの対話記録が【資料2】である。+3の項が左辺に増えたことと、両辺から3引けば、3x=6に帰着できることに気づくことができた。
【資料1】のように方程式を縦に並べて提示したことと、2つの方程式の違いを見つける活動を行ったことで、見通しをもつことができた。

教師:2つの方程式どこが違うでしょう。
生徒A:左辺が多い。
生徒B:項が多い。
教師:項って言葉がいいね。数学の言葉だね。具体的には、どこのこと?
生徒全員:+3。
生徒A:+3がなくなれば、(左辺が)3xになるのにな。
生徒C:+3の分だけ引けばいいんだ!
生徒A:え?あ、そういうこと?
教師:Cさんの言ったこと分かったかな?もう一度言ってみて。
生徒D:だから、3引けばいいんだよ。
生徒E:あ、両辺から、両辺から!等式の性質を使う!
生徒A:なんだ、2x+3=9の両方に-3をすれば2x=6になるんだね。
(2)典型的な誤答の提示
次に、「3x+20=5」を提示し、習熟を図った。
見通しをもつときに、先の問題の考えを使って「両辺から20引く」、「両辺を÷3する」という2つのアイデアが出てきた。
「両辺から20引く」解き方を全体で確認した後、「両辺を÷3する」アイデアをわざと間違えて板書し【資料3】、生徒に提示した。
そのときの対話記録が【資料4】である。
誤答を提示したことで、「等式の性質」についての確認と、どこを間違えたか考え直すことができた。
また、「両辺を最初に÷3する」デメリットも生徒に感じさせることができた。
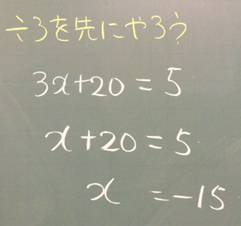
教師:x=〇ってするのが目標だから、÷3して、【資料3】のようになったよ。これもいいよね?
生徒C:解が違うね。
生徒A:でも間違ってないよね?
生徒B:待って、右辺は÷3をしてないよ。じゃない?
生徒D:うわ、面倒。
生徒A:でも、これ、x=3にならなくない?
生徒E:あってそうなのにー。
教師:どこを÷3するんだっけ?
生徒F:両辺。
生徒A:20を÷3をしてないのか。
生徒B:数字の部分は、分数になるのか。面倒くさいな。
教師:でも、先に両辺をすべて÷20すれば解けるよね。みんなだったらどっちでやる?
生徒全員:分数がでない方。両辺から先に20を引いた方が楽。
(3)x=3になる方程式を作ろう
最後に、【資料1】の例題を用いて、「x=3から2x+3=9をどのように作ったか。」発問した。
上から順に「両辺を×2→両辺に3を足す」ことを生徒と確認をした。
次に、「x=3になる方程式を作ろう」と発問した。
生徒たちは、「―15x+38=-7」や「0.1x+2.7=3」、「8/3 x+5=13」、「2/5 x+1/2=9/10」といった問題を考えた。
この問題は次の時間に取り扱った。
前時の【資料3】の学習から、方程式の解法を逆に考えて、両辺の分母をはらうように計算すれば楽なことを見つけることができた。
成果及び課題
○成果
- 「2x=6」と「2x+3=9」の方程式を比べてそれぞれの方程式の違いを明確にしたことは、「両辺から3引けば、習った形に帰着できる」という生徒の発言を引き出せた。有効に働いた。
- 「両辺を÷3」する誤答を提示したことは、間違いを見つけて自分の力で直したり、よりよい解法を考えたりする場をつくれた。有効に働いた。
- 「x=3になる方程式」を作ったことは、分数や小数が含まれる方程式を簡単にするために、「両辺を〇倍する」考えを生徒から引き出すことにつながった。有効に働いた。
○課題
・本授業は、移項する意味の指導が形式的になってしまっている例年の授業の反省から構想したものである。
「x=3になる方程式」を作る中で、どんな操作をすれば、方程式を作れるかをみんなで確認し、次時でどうやって解くかを確認し、最後に移項の意味を知る流れを想定していた。生徒の振り返りを読むと、いかにして方程式を効率よく解くかを意識していた。
誤答を提示したことが原因だった。
等式の性質を使って方程式を作り出したり、友達の問題の作り方を考えたりすることに重点をおいけば、ねらいにもっと迫ることができた。
生徒の意識の流れを想定して今後教材研究に励みたい。
・x=3になる方程式を作るときに、生徒は、両辺に数を足したり、割ったりしていた。
そこで、両辺にxを足したり、引いたりすることを教師が示すと、もっと学習に広がりがでたと考える。
そうすれば、教科書で取り扱われる一次方程式のすべての計算を、生徒の考えた問題を使って取り組むことができただろう。来年度の授業に活かしていきたい。
参考
・玉置崇(2014)「わかる!楽しい!中学校数学授業のネタ100 1年」.明治図書.P58





コメント