今日は、標本調査の話です。
なんで、標本調査の話なのに、キャッチ画像が、味噌汁なのとツッコミが入りそうですが関連してます!
落語家の立川志の輔が噺のまくらで、標本調査の例え話をしていました。
これ、子どもに話すとウケがいいです。
標本調査の単元は受験間近で、サラッと流してしまいがちです。
少しでも子どもの頭に残るように話したいですね。
選挙の話を使って
国政選挙の時に、20時に選挙の投票がおわって、どの局も、選挙特番になりますよね。
それで、
「選挙特番です。まず当選確実の議員の発表です」
ってみて、不思議だなって思ったことありませんか?
隣には開票率0パーセント。全く投票結果を確認してない状態ですよ。
それで当選確実って出るのおかしくないですか?
もちろんカラクリがあります。
そこには今から勉強する数学が使われています。
さて、どうやっているでしょう?
実はこっそり個別に聞いている
もちろん、開票前に、こっそり選挙箱の中を見ることはできません。
じゃあどうするか。
皆さんわかりますか?
それは、選挙所の出口で記者が待っていて、出てきた人一人一人に、
「誰に投票しましたか?」
と聞くんです。
そうすればだいたいの傾向や誰が当選するかはみなさんだって予想出来るでしょ?
これを出口調査といいます。
ただ、これでは、信憑性はありません。
そこで数学の力を使うことで、確実に当たるようにするのです。
どうやって確実に当たるようにするのかな?
さぁ、どうすれば確実に当たるようになるでしょう?
・・・そうすると子どもからは
- たくさんの人から聞く
- いろんな場所で聞く
- いろんな人から聞く
といった対応が出てきます。
- たくさんの人から聞く
という意見からは、極端な事言えば投票した人全員に聞けば、誰が当選したか分かる。
という意見です。
その通りです。
ただ、子どもに問い返します。
「できる?」
そりゃできませんよね。それができるなら、困りません(笑)
- いろんな場所で聞く
これはぜひ子どもに考えさせたい意見です。
なぜ、いろんな場所で聞く必要があるんでしょう。
東京と大阪では、投票した人の考え方が違うから、当選させたい議員も変わってきます。
だからいろんな場所で出口調査をする必要が出てくるのは自明です。
- いろんな人から聞く
も良い意見です。ただ、いろんな人とはどういう人なのか、ぜひ問い返したいですね。
今回引き出したいのは、老若男女いろんな人から聞かなければいけないという必要性を子どもに気づかせたいものです。
用語の確認と味噌汁の話
今回の話では、
母集団→有権者
標本→出口調査をした人
になります。
ここで、閑話休題。
味噌汁の話をします。
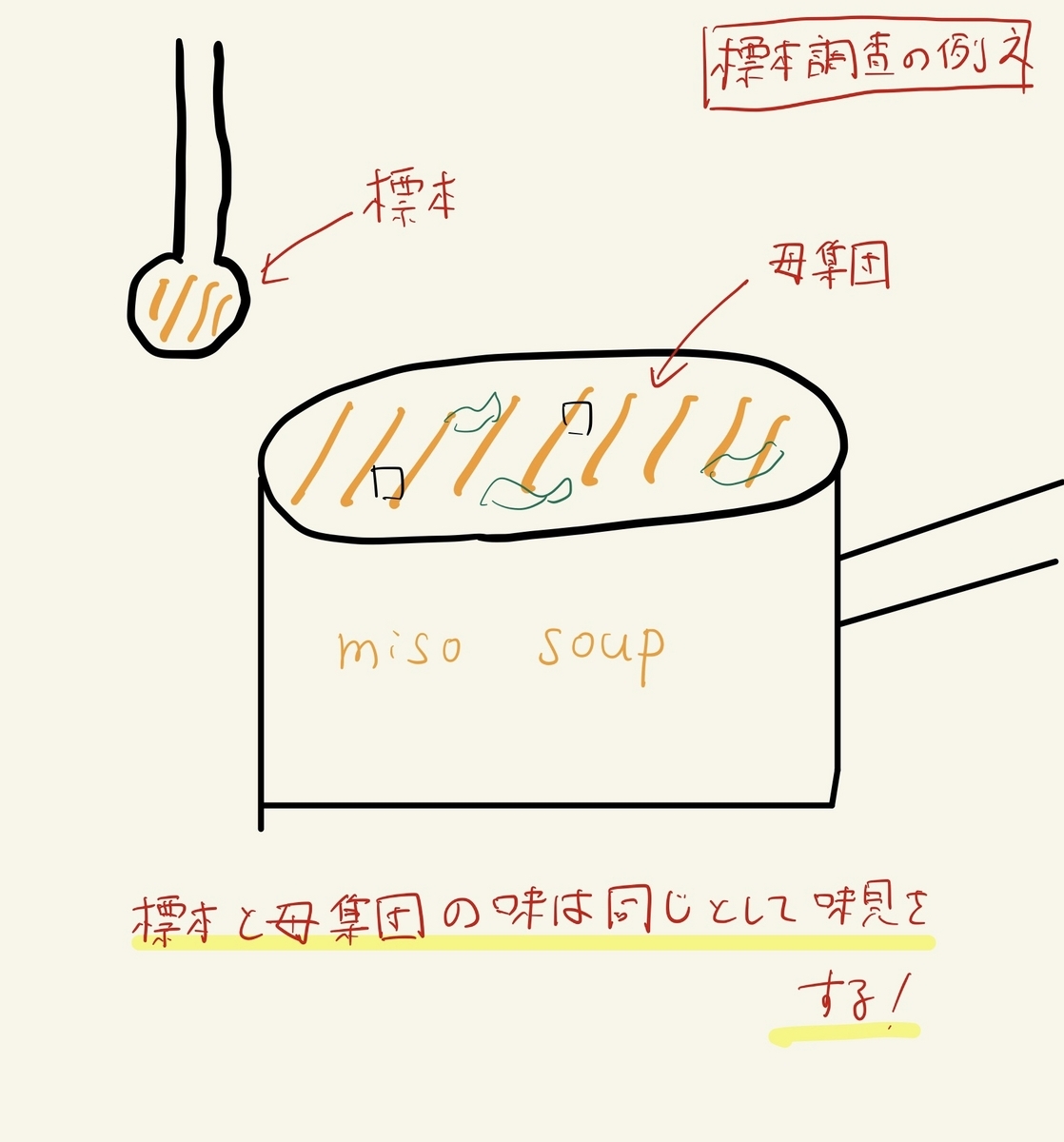
ところで皆さん、家で味噌汁作るでしょ?
味噌汁を家族に出す前に味見するでしょ?
全部、飲む?
飲まないよね。
ひと匙とって、フーフーして舐めてみる。
このひと匙が、標本なのよ。
そして、取り出した味噌汁が、母集団になる訳。
ただ、味見する時に気をつけなきゃいかんことあるよね。
そう。
よく味噌汁を混ぜなきないけないよね。
味噌がそこにたまっていて、上澄みだけ取ったら味が違うかもしれない。
だから、混ぜる必要があるのよ。
さっき選挙の出口調査をする時に、
いろんな場所で、いろんな人から話を聞く必要があるって気づいたよね。
それが、味噌汁のかき混ぜることに相当するの。
これを「無作為に抽出する」っていいます。
ここでクイズ
標本調査は、母集団の一部を標本として取り出して、だいたいこうなるだろうと予想する調査のことをいいます。
逆に、母集団全員に聞く調査は全数調査と言います。
今から言う調査は、標本調査でしょうか?全数調査でしょうか?
(ここは授業の最初に子どもから知ってる調査を聞いておいて、ここで再度出すと盛り上がります。)
- テレビでやっている、中学生の好きな芸能人ランキング
- 自分の中学校の期末テスト
- 高校入試、大学入試
- (一般的な)川の水質調査
- 池の水を全部ぬく番組の調査
- 学校で皆さんがやる健康診断
みなさんは、どっちだと思いますか?
理由も聞くと、結構面白いですよ!
ちなみに私のクラスではこんな理由が出てきました。
答えも載せておきます。
- テレビでやっている、中学生の好きな芸能人ランキング→標本調査
中学生って言ってるのに、私のところに調査はきてないから。
- 自分の中学校の期末テスト→全数調査
受けなきゃ成績つけてくれないじゃん。欠席したら、別室でテスト受けるし。
- 高校入試、大学入試→全数調査
仮に志望者を標本調査して、標本に選ばれた人が不合格だったら、標本にもれた人も不合格。逆に標本が合格だったら、普通なら入れない高校に願書だけ出したら僕も合格になるじゃん。
標本調査じゃ無理だよ(笑)
- (一般的な)川の水質調査→標本調査
- 池の水を全部ぬく番組の生き物調査→全数調査
池の水を全部抜けばそりゃ、生き物調査確実に出来るから全数調査。
でも流れている川の水を全数調査しようなんて無理!
- 健康診断→全数調査
標本の人が例えば、重病だったとしたら、俺のクラスみんな重病ってことになるでしょ。
逆に標本みんな健康だったら、みんな健康って言われてもおかしいよね。
だから全数調査するしかない。
こんな感じで理由も子どもに話させると、結構面白いです。
反例のような話も出てきます。
味噌汁の話をすると、後の学習で生きる
この後、標本から全体の様子を確認する問題が出てきます。
比を使って解くことになりますが、味噌汁の話がここで生きてきます。
味噌汁の全体も味見のひと匙も、「味が変わらない」
つまり傾向が一緒である。
と、子どもは何となくイメージがついているからです。
クラス全員がサラッと解けました。
まとめ
いかがだったでしょうか?
上手く生徒の知っている調査を引き出して、具体的な話と、抽象を結び付けられると良いですね。
もし良かったら使ってみてください。





コメント