中1で素因数分解を勉強します。
割り算の筆算記号をひっくり返して、商を下に下に書いていくあの計算です(下図)。
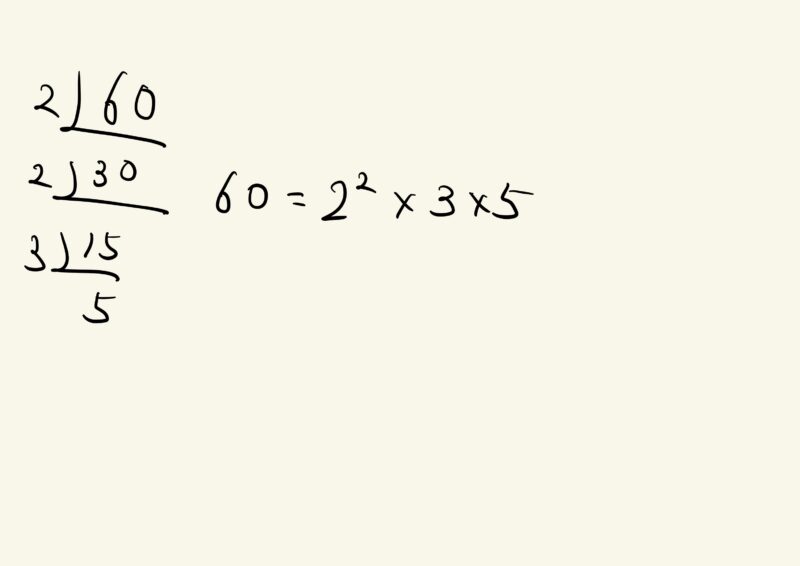
素因数分解以外では使わないのかなと思っていたら、プログラミングで出てきました。
10進数を2進数に変換するときに使うんですね。(基数変換と言います)
自分は中学の時に、基数変換の仕方を筆算でやれることを教えてもらいませんでした。
ちょっと感動したので、記事にします。
現行の高校の教科書を読んでいないので、「指導案」と銘打っていますが、ずれていたらごめんなさい。
ねらい
10進数で表した数を、n進数に変換できる。
n進数で表した数を、10進数に変換できる。
授業の流れ
10進数とはなんだろうか
今日は1234という数を見てようと思う。
よく小学校では、数え棒を使って数を見てきた。
「1234という数はどういう数だろうか?」
- 1が1234個集まった数
- 1000が1個、100が2個、10が3個、1が4個集まった数
このように言うことができるだろう。
1、2、3、4それぞれの数の場所を、1000の位、100の位、10の位、1の位とも呼んだ。
式を使って表すと、$1234=1×10^3+2×10^2+3×10^1+4×10^1$と言うことだ。
つまり、1000の位、100の位、10の位、1の位はそれぞれ、$10^3$の位、$10^2$の位、$10^1$の位、$10^0$の位と言っても良いことがわかる。
この10のことを、10進法の基数(または底)ということとする。
基数10の右肩に乗っている数(指数)が3、2、1、0と規則的になっているということがわかる。
2進数とはなんだろうか
先の流れから2進数を考えてみよう。
2進数とは「基数が2になった数」である。
- 使う数字は0と1だけ
- 1の位、2の位、$2^2=4$の位、$2^3=8$の位と表す
ことが類推できる。
よく2進数は、PCを制御する上で使われるのである。
人間のようにPCは10進数を理解することができないのだ。(PCはそんなに頭が柔らかくない)
基数変換
PCは10進数を2進数にどう変換しているのだろうか(これを基数変換という)。
実は、中1で勉強してきた素因数分解のテクニックを応用して変換している。
素因数分解では、素数で指定された数を割りすすんで行ったが、今回は、「基底(2)で割り進む」ことにする。
例として、60を取り上げてみよう。
下図のように60を2で割り続ける(60を2で割り、その商30を2で割り、さらに商15を2で割り・・・)
そして、それぞれ2で割ったときに余りが「1になる」か、「0になる(割り切れる)」かを調べる。
得られた余りの列(1と0の列)を下から読んでいくと2進数での表記になる。
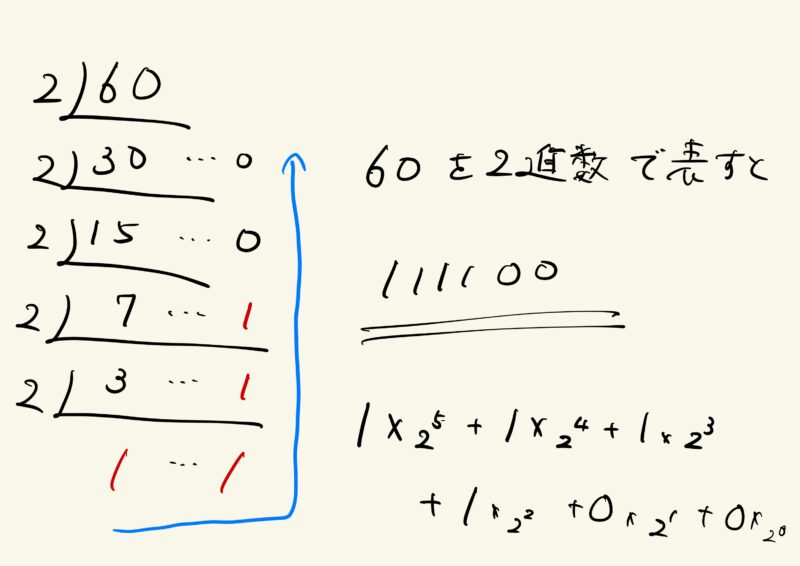
図にも書いたが、60を2進数表記にして、各位に分けて書くと
$60=111100=1×2^5+1×2^4+1×2^3+1×2^2+0×2^1+0×2^0$と分解できることがわかります。
PCの計算は、人間が書いた10進数の計算式を2進数の計算式に変換して、2進数で答えを出します。
それでは、人間は分かりにくいので、答えの2進数を10進数に変換し直して我々に分かりやすい形で示してくれているのです。
最後に(皆さんに質問)

最後に皆さんに質問です。
「2進数 10101を10進数で表すと幾つになりますか?」
「10進数 60を3進数や4進数に基数変換したい時には、どのような手続きをすれば良いですか?」
「2進数や10進数は位取り記数法という表記です。では、位取り記数法を使わない数の表し方もあるのでしょうか?」
もし分かったら、ぜひコメントをくださいね。

【中1 素因数分解の指導はこんなかたちでやりました。合わせてご覧ください】






コメント