数学なんて、社会に出たらいらない!とよく言われます。
生徒にも面と向かって言われたことがありました。
確かに中1、中2レベルならいざ知らず、中3、高校レベルの数学にまでなると、社会に出て使うか?と言われたら表面上は使いません。(お前が持っているスマホなんて、数学の塊だぞこの野郎!ということは大人なので言わないことにしておきます。)
そうした時に、数学の学習で何を学ぶのかとということの一つに「一般化、抽象化」の考えができるようになることだと思っています。
数学は、積み上げの学問と言われています。
それは、今まで習ったことを土台に、新しい課題に対してチャレンジをしていくからです。
知っている知識を使って、さらに一般化・抽象化できないか?と、どんどん数学の世界を広げていくことが、学校で習う数学として大切だと考えます。
この感覚を掴むことができれば、学校で取り扱う問題は、解けるようになると考えています。
中学校3年生の最初に行う「式の展開」の分野は、今まで学習してきたことを使って、拡張していくとても楽しい単元だと思っています。
皆さんはどのように授業をやっていますか?
今回は、その授業の記録をお伝えします。
教材研究

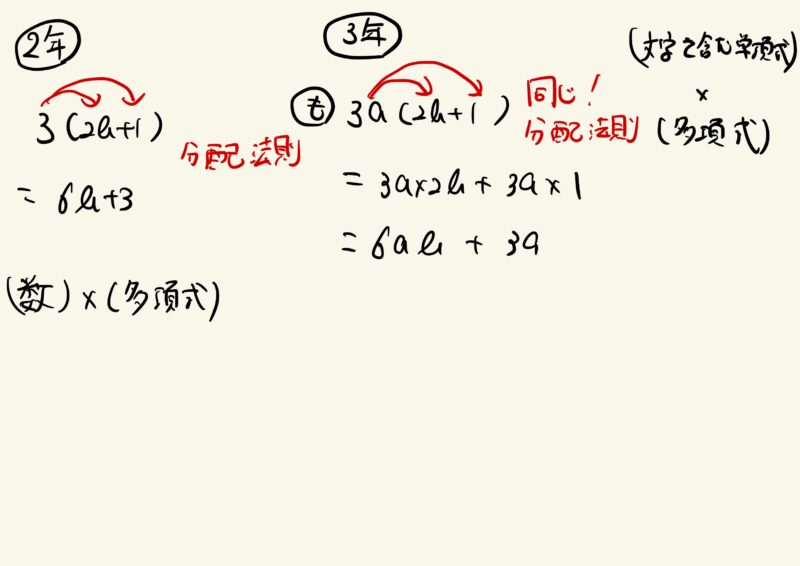
中学2年では、(整数)×(多項式)を勉強します。
例1:$3(2x+1)=6x+3$
中学校3年では、(単項式)×(多項式)を勉強し、そのあと(多項式)×(多項式)へと進んでいきます。
例2:$3a(2b+1)=6ab+3a$
例3:$(a+b)(c-d)=ac-ad+bc-bd$
この3つの問題を解くために共通して必要な知識はなんでしょうか?
そうです。分配法則です。
そこに気づくか、抽象化、一般化ができるかどうかなのです。ただ、生徒はいろんなところでつまづきます。
例えば、例2だと「3が$3a$という文字になるだけでフリーズしてしまう」、例3だと、「二つも多項式になってしまって、もうどう計算すればいいか全く想像がつかない」となってしまう子も多いです。
とにかく安心させてあげること、同じようにやればいいんだよと伝えることが大事だと思っています。
授業の実際
まずは、去年の勉強した内容を復習しました。

分配法則を使うことで、それぞれの項と掛け合わせることを確認します。
「3年生では、こんな問題を解きます」と、$3a(2b+1)$を提示します。
ここで、やってみましょうと促します。
ここで動けない生徒は、何を使えばいいかがわかっていないのです。
だから、個別に、(多ければ黒板の前で)「さっきと何が違う?、そうだね、3が3aになったよね。でも他は一緒じゃん。何を使えばいいと思う?そうそう分配法則だね。」と前に進む勇気をつけてあげればいいです。
そして、次に(多項式)×(多項式)の問題を提示します。
ここでは、分配法則を使うことをすぐ想起するのは難しいと思います。
でも、授業の流れから分配法則を使いたいなぁと思わせるのは大事です。
私は合ってなくてもいいので「どう計算すればいいと思う?」と予想させます。
あーだこーだ言いながら、それぞれ掛け合わせるというアイデアが出てこれば、正解!としてしまいます。
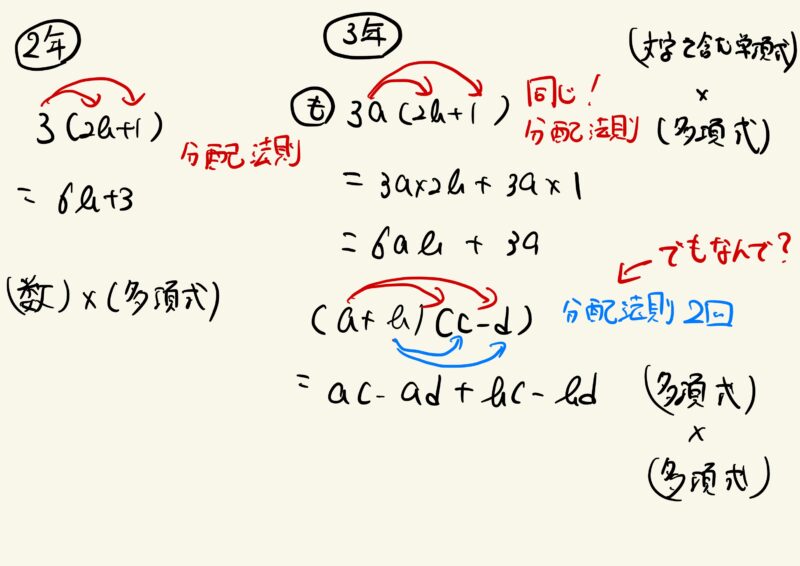
ここで「実はそれぞれ掛け合わせればいいんだけど、そんな分配法則やってないよね。どうしてこれでいいと思う?」と後から理由を肉付けをしていくようにしていきます。
考えさせるポイントは、(単項式)×(多項式)なら、分配法則が使えた。(多項式)×(多項式)を(単項式)×(多項式)に変えて、「同じようにみて」分配法則が使えないかな?と視点を与えて考えさせるのです。
そうすると、$M=(a-b)$と置換をするアイデアが出てくるかもしれません。(出てこなくても気にしません。これは、教えてあげてもいいと思います)
そうして、(多項式)×(多項式)の分配法則のやり方を落としていくのです。
「置換」の指導は導入でしっかりやっておく
この「置換」のアイデアはとても大切にしていて、丁寧に授業で取り上げます。
展開の授業を進めていくと、$(a+b-2)^2$のような問題が出てきます。
この問題をどう解くのでしょうか?
ここで置換のアイデアが生きてきます。
$M=a+b$として、$(M+2)^2$とすれば、公式が使えます。
このように、知っている形に置き換えることで展開(この後の因数分解)が解きやすくなるのです。
その必然性を出すためにも、展開の序盤で「置換」のアイデアの種を子どもに蒔いておきます。
最後に

いかがでしょうか?
それぞれの単元で考えを発展させていくために大切なアイデアがあります。
今回の「展開」の単元では、「分配法則」と「置換」が大事なアイデアです。
この考えを、単元を貫いて指導をすることで、生徒は見通しを持ちながら学習に取り組むことができます。
教師としても、何を大切にするかを考えながら教材研究できるといいですね。
皆さんはここでの授業をどのように行なっていますか?
ぜひ、教えてください。

乗法の公式の導入について、こちらで授業についての考えを書いています。ぜひ合わせてご覧ください!
展開・因数分解の利用については、こちらの記事で紹介しています。






コメント