一次方程式は、今までの計算と少し趣が変わります。
いままでは、$1+2=3$のように、左から右に式が流れていくイメージでした。
方程式は違います。
$x+2=3$を等式の形を保ったまま、等式の性質を使って、式変形をして解を求めていきます。
式が上から下に流れていくイメージです。
そこのイメージをどれだけ作っていくかがこの単元の肝になっている感じています。
一次方程式をつくるというイメージでの授業案はこちら!
方程式のイメージは天秤
方程式は、「未知数を表す文字を含む等式のこと」を言います。
つまり、等式であるということが大前提なのです。
等式は、「2つ(左辺と右辺)の数量が等しい関係を表した式」です。
そこで、方程式は天秤というイメージを子どもに持たせます。
教科書でも以下のようなイメージ図が載っています。

このイメージ図ならわかりやすいですし、両辺から同じものを差っ引くこと(等式の性質)を子どもが気付きやすいです。
ただ、これ毎回描くのは大変なので、式を天秤にのせて、以下のようなイメージを生徒につけるようにしています。
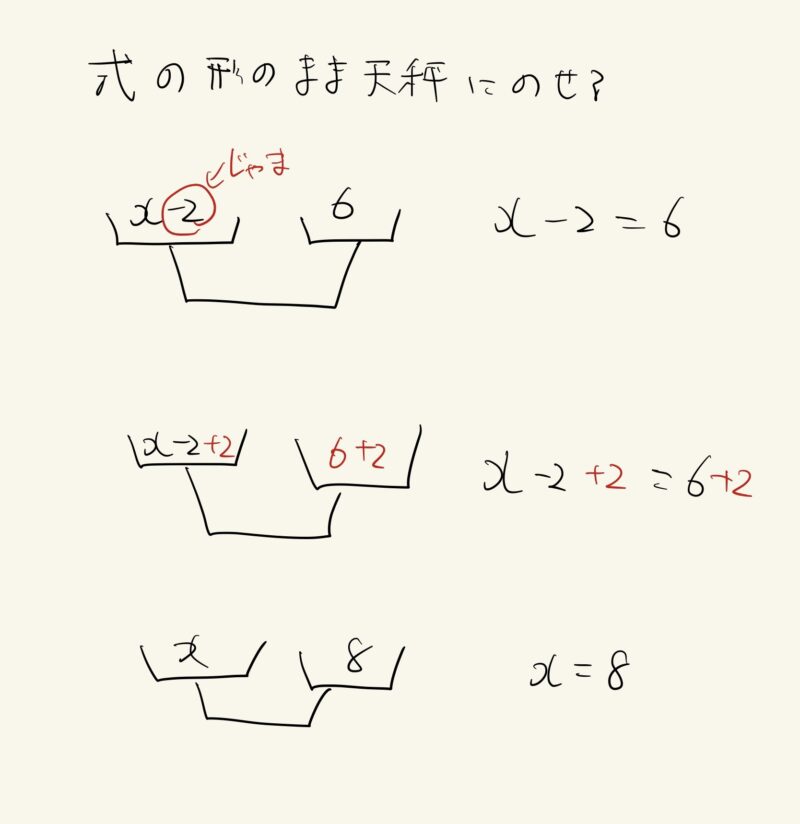
これの何がいいかというと、$3x=2x+5$のように$x$を操作しなければならない場合に有効です。
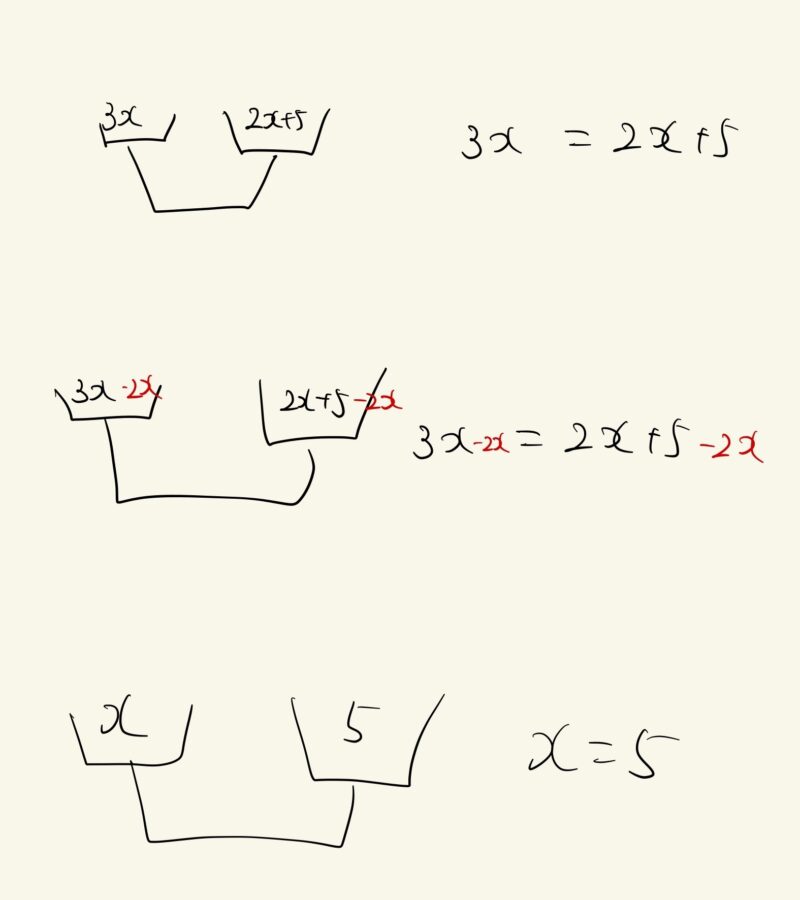
$3x+2=8$のような問題は等式の性質を使って問題なく生徒は解けました。
そんな子供たちも、文字に対しては等式の性質を使っていいのか?と思考がストップしてしまいました。
そのときに、上のイメージ図を提示したら、子どもは動き出すことができました。
方程式で大切なのは、「天秤のつり合いを保ったまま、式変形をしていくこと」なのです。
両辺をそっくり入れかえる場合でも
啓林館では、以下の問題も取り扱われています。
かりんさんは、方程式$8=3x+5$の解き方を次のように説明しました。
「左辺と右辺を入れかえてから、左辺を文字の項だけに、右辺を数の項だけにするために、5を移項して、方程式を解きました」
(1)かりんさんの方法で、この方程式を解きましょう
(2)5を移項できる理由を説明しましょう。
(3)左辺と右辺を入れかえるとどんなよさがあるのかな?
啓林館.「未来へ広がる数学1」.p93
この場合でも、天秤のイメージさえあれば説明がつきますね。
早く簡単に方程式を解くためにも、付けておきたいイメージです。
まとめ
今回は、「天秤」をトピックとして、方程式の解き方を考えました。
数学を言語化すること、イメージ化することっは上達への必須事項だと考えています。
少しでも数学が苦手な子の力になればと思います。




コメント