今年は、対頂角、同位角、錯角の導入をすごく丁寧にやりました。
生徒達の反応が良かったので、授業の流れを紹介します。
ねらい
直線を1本、2本、3本とかく中でできる角について、同じ大きさの角を見つけることができる。
授業の実際

問(1)「直線を1本引きます。ここにはどんな角があるでしょうか。」
これは、直線の上と、下に180度の角ができますね。
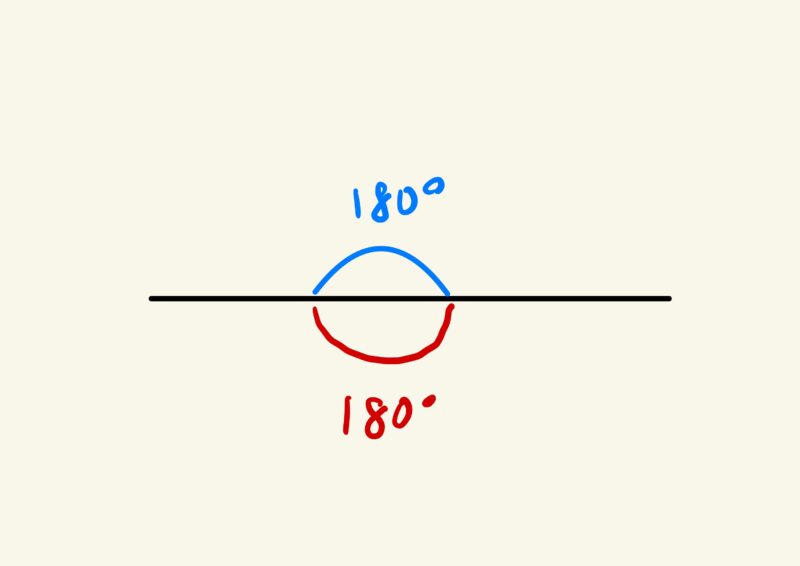
クラスのみんな、すんなり納得しました。
問(2)「直線を2本引く。ここにはどんな角ができますか?」
生徒から出てきた答えは、
「角ができない(平行)」、「交わる」、「垂直」と出てきました。

生徒は、「交わる」と「垂直」を別に分けていたので、今後の授業の流れのために、「垂直は、交わる場合の特別な形」であることを確認して同一にすることにしました。
追加で次のような発問をしました。
問(2)−1「『交わる』関係にあるとき、図の中にある角の間にはどんな関係があるでしょうか?」
生徒は、「向かい合っている角が等しい」とすぐに答えました。
そこで、「向かい合っている角ってどこのこと?」と聞くと、しどろもどろになる生徒が何人かいました。
ここで、図に向かい合っている角を黒板の図にチェックをしてもらって、「向かい合う角はここだよ。確かに等しくみえるね。」と念押ししました。

「向かい合う」という言葉は当たり前だと感じがちですが、数学で出てくると混乱する子も何人もいます。
新しい言葉が出てきたらしっかり確認することが大切です。
問(3)「平行な2直線に交わるように、さらにもう1本直線を引きます。この図の中でできる角はどんな関係にあるでしょうか?」
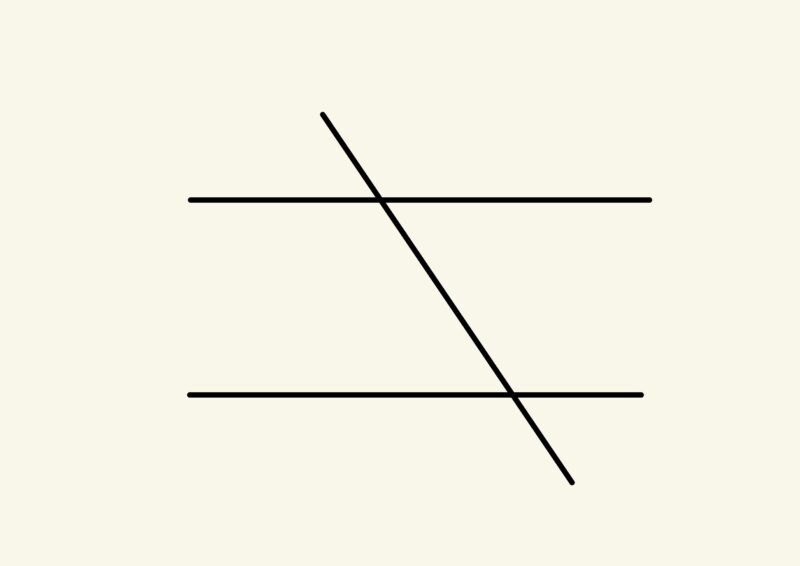
ここでも見た目から次のように同じ角度を見つける事ができました。
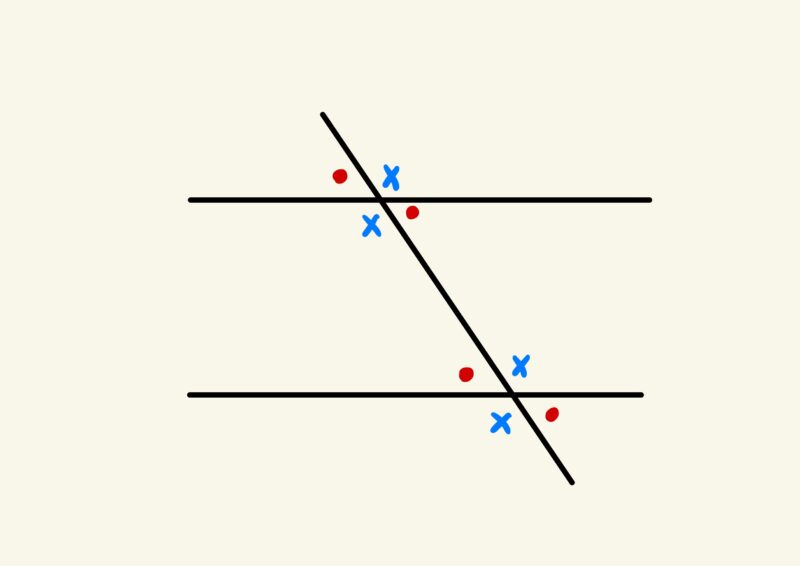
授業の終末
「今、直線が2本と、3本の場合で同じ角が出てくることを見つけました。
でも、何で同じと言えるのかな?
それを誰も反論できないように、順番に説明する方法を考えていきます。
証明といいます。次から考えていきましょう。」
と授業を終わりました。
この授業のポイント

この授業は、3つの良いポイントがあると考えます。
- 直線を1つずつ増やしていくことで、角についてどんな事が言えるか「What-if-notのストラテジー」で数学の概念を拡張していること
- (数学な苦手な子にとって)図をかいて、「同じ大きさの角」を見つける課題にして、みんなが取り組みやすい問題構成になっていること
- 直線が2本、3本の場合、直線の引き方を変えても、全く同じ事が言えるか確認する余地が残っていて、実際に証明する必要感が出てくることを感じやすいこと
ちなみに、問題を書いた後、図は最初、黒板に書きませんでした。
問題を提示して、生徒に「問題の通り、図をかきましょう。」と指示をして、隣の生徒と見比べるようにしました。
問題文から適切に図をかく力も大切だと考えています。
特に、直線を2本引いた場合、交わる場合と、交わらない場合(平行)が出てくることも、図をかかなければ、なかなか気づきません。
そうやって、数学力を育みたいと思っています。
最後に
このあとは、対頂角・同位角・錯角の証明に入っていきます。
対頂角はいいのですが、同位角・錯角の証明はすごく曖昧です(だから教科書では「説明しましょう」という記述になっていますが)。
自分もこのふわっとした説明では、腑に落ちないので、「ユーグリットの原論」の5つの公準を伝えて、生徒に説明する活動を作っています。
難しいと思われるかもしれませんが、結構、生徒は公準を使って説明しようとがんばります。
実は中1の図形分野でも、私は説明するようにしています。
少しでも生徒の理解につながればいいなと考えています。
もし、私もユークリッドの原論に言及して授業しているよという方がいたら、教えてください。

参考文献・参考HP
参考文献
「未来へ広がる数学2」.啓林館.pp94~pp95
参考HP








コメント