主題設定の理由
生徒の実態
本学級では、「隣の友達と考えを交流しましょう」と指示すると、進んで友達に話しかけ、話し合いを始める生徒が多くいる。
また、生徒Aをはじめ自分の考えをもつことが難しい生徒も、友達の意見を参考にしようと真剣に友達の話を聞く。
このように、1年生は友達と話し合いを進め、みんなで数学をできるようになりたいとがんばることのできるクラスである。
「文字の式 代入」の学習では、「3a+5にa=2を代入した値を求める」学習を取り扱った。
”a”と書いた紙をクリアファイルに入れて、その紙を2に入れ替えることで、代入の意味を視覚的に分かるように教材を作成した。
すると、生徒Aは、文字の部分を「数字が入る箱」と捉え、文字の部分を数字に変えて計算をするとよいと理解することができた。
このような生徒の実態から、子どもたちが関数の意味を理解するためには、視覚的に分かる教材・教具を用意することが大切であると考えた。
研究の仮説と手だて
仮説と手だて
【仮説】
ICTを活用し、視覚的な支援を行えば、関数について意味を理解しやすくなったり、関数の特徴を見つけたりすることができるようになるだろう。
【仮説に対する手だて】
手だてⅠ:比例関係にある動画を視聴させ、関数についての理解をイメージしやすくさせる。
手だてⅡ:比例定数を生徒に決めさせ、タブレット上で複数グラフをかかせることで、比例定数とグラフの関係性を捉えられるようにする。
手だてⅢ:グラフの変化を、ICTを活用して動的に見せ、比例定数とグラフの関係を捉えることができるようにする。
手だてⅣ:反比例のグラフの特徴を表と関わらせて捉えることができるようにするために、アプリでグラフが曲線になることを見せる。
検証方法
本単元は、小学校で学習した比例・反比例の概念を、負の数まで拡張し学習をする。
生徒の実態を踏まえ、本研究では、視覚的にわかる教材・教具として、ICTを活用する方法を検討する。
ICTを教具として活用することで、生徒がどんな話し合いをして、関数についての理解を深めていくのかを看取りたい。
まず、手だてⅠとして、関数の概念を生徒が理解しやすくなるよう、水槽に水がたまる動画を視聴させる。
教科書の挿絵や文章を見るよりも、動的に変化をみることができるので、関数の意味を理解しやすくなるだろう。
動画を視聴させた後、生徒が関数についてどんなイメージをもったのか、話し合いの中で生徒の理解を観察する。
手だてⅡ、Ⅲは実際に比例のグラフをかく場面において、グラフの概念を生徒が獲得するための支援として手だてを講じる。
タブレット上でグラフを瞬時にたくさんかけるので、生徒はグラフを観察し、グラフの特徴について考えをもちやすくなるのではないかと考える。
使用するアプリについては「Geogebra関数」を利用する。タブレットを利用した時の生徒の反応を看取り記述する。
抽出生徒Aについて
略
単元構想(16時間完了)【資料1】
【最終稿】単元構想(変化と対応)研究の実際
動画を視聴し、関数の定義を獲得する生徒A(第1時)・・・手立てⅠ
関数の意味理解の導入として、水槽に水がたまる動画を視聴させた【資料2】。
【資料2】水槽に水がたまる動画

次に、生徒に「時間がたつと変わるものは何?」と尋ねたところ、【資料3】のように意見が出てきた。
【資料3】生徒達の反応
時間がたつと‥
- 水が増える(生徒A)
- 水の色の濃さがかわる
- 重くなる
- 水の入っていない場所が減る
- 1分に2目盛り分ずつ増えている。
生徒Aは「時間がたつと、水が増える」と回答している。
生徒の実態でも述べた通り、そもそも生徒Aは関数の意味は分かっていなかった。
動画を視聴させたことにより関数の定義である「x(時間)の値が決まると、y(水)の値が1つに決まる関係」について生徒Aが例示をして、確かに理解していることが見て取れる。
この時間の生徒Aの振り返りが【資料4】である。
【資料4】生徒Aの振り返り

生徒の記述にあるように「『○○が変わると、○○になる』ものが関数」であると、自分の言葉で関数について表現できている。
関数関係を具体的にイメージさせるために動画を視聴させたことは有効であった。
手だてⅠは有効に働いた。
複数のグラフをかき、比例定数とグラフの関係を理解する生徒A(第8時)・・・手立てⅡ
この時間は、y=2xのグラフのかき方を学習した次の時間である。
比例定数の数字を自分で決定し、タブレット上で関数の式を打ち込みグラフをかくという授業を行った。
比例定数が変わることで、グラフの概形はどうなるか生徒が発見することをねらいとしている。
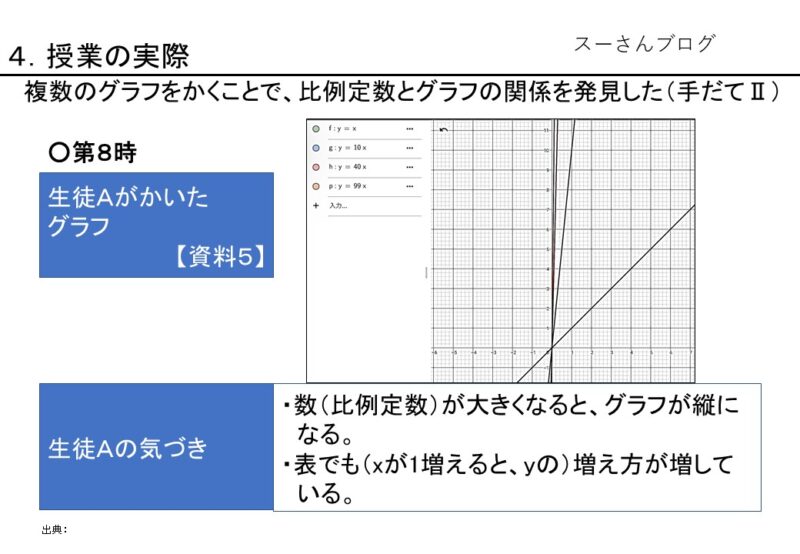
生徒Aは、【資料5】のようなグラフをタブレット上でかいた。
【資料5】生徒Aのかいたグラフ
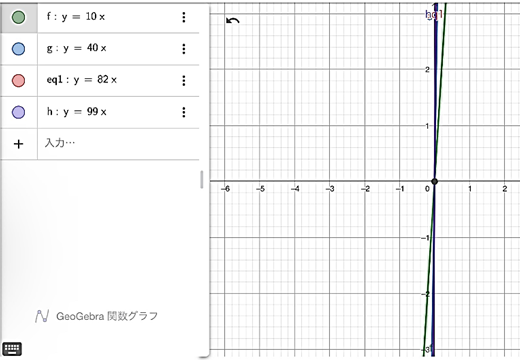
このとき生徒Aに「何か気づいたことはあるか」尋ねたところ、「数(比例定数)が大きくなると、グラフが縦になる」ことに気づいていた。
その後、5人のグループで気づいたことを発表しあった。
そこで、生徒Aは比例定数が小数になっているグラフを友達から見せてもらって、説明を聞いた。
話し合いが終わった後、発見したことを各グループの代表が発言し、クラス全体で意見交流する時間をもった。
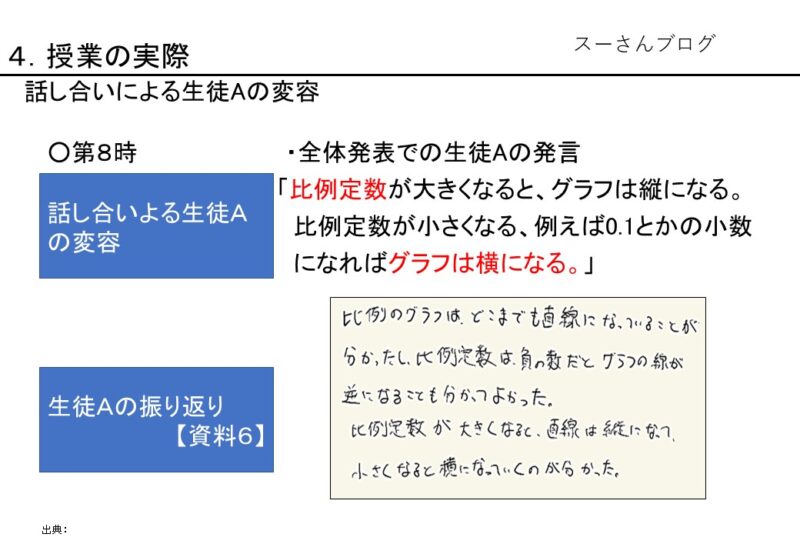
そこで、生徒Aは代表として「比例定数が大きくなると、グラフは縦になる。比例定数が小さくなる、例えば0.1とかの小数になれば、グラフは横になる」と発言をした。
生徒Aは一人で考えたときは、「数(比例定数)が大きくなると、グラフが縦になるということ」しか気づいていなかった。
そこで、友達のグラフを見せてもらって、話を聞いたことで「『比例定数』という言葉を獲得して実際に使用できた」こと、「比例定数が小さくなると、グラフの概形はどうなるか」まで理解が深まっていることが分かる。
鉛筆でノートにグラフをかくこともできたが、生徒Aにとっては時間がかかり、複数のグラフを時間内にかき、考察し、意見交換をするというのはハードルが高い。
タブレットでグラフをかいたことで、考察の時間を十分にとることができたから、自分の考えをもち友達と意見交流をするなかで比例のグラフの特徴を新たにつかむことができたと考える。
生徒Aの本時の振り返りは、【資料6】である。
【資料6】生徒Aの振り返り

ここからも生徒Aは比例定数の数によって、グラフの傾きがどうなるかを理解していることが確かに分かる。
手だてⅡは有効に働いたといえる。
比例のグラフの特徴をつかむ生徒A(第9時)・・・手立てⅢ
前時(第8時)で生徒たちからでてきた比例のグラフの特徴は、【資料7】のとおりである。
【資料7】生徒達の見つけた比例のグラフの特徴
- 比例定数が大きくなるとグラフが縦になる。逆に小さくなると、グラフが横になる。(生徒A)
- 比例定数が負の数になると、傾きが逆になる→右下がりのグラフになる
- 比例は、直線のグラフである。
比例のグラフは必ず原点を通るという発見は、時間内に意見として出てこず、唯一生徒Bだけが、「比例定数を変えて、グラフをたくさんかくと、原点を中心に、花火のような『「放射線状の模様』がかけるのではないか」と書いてきたにとどまった。
「グラフをかく」活動だけでは、必ず原点を通るという比例のグラフの特徴が発見しづらいと執筆者は考えた。
また、生徒Bの「放射線状の模様」が描けるというのはとても面白い発想である。
この考えを他の生徒に味わわせたいと考え、ICTを使って教材化をした。
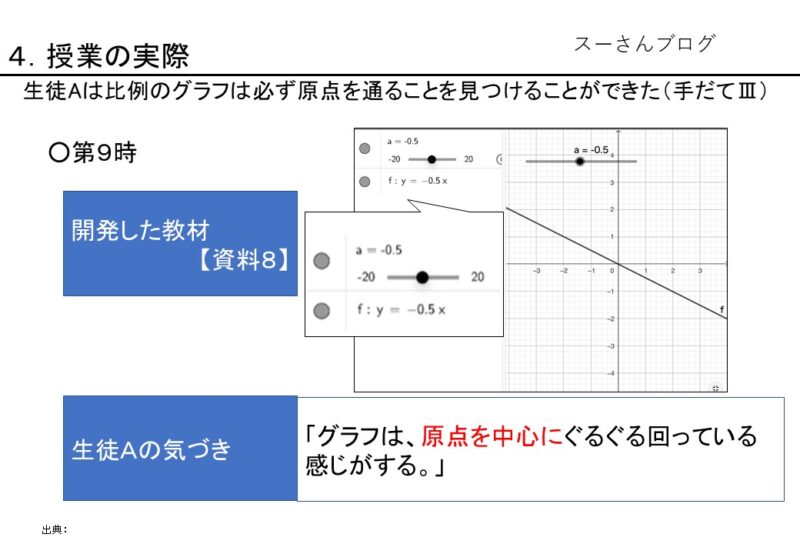
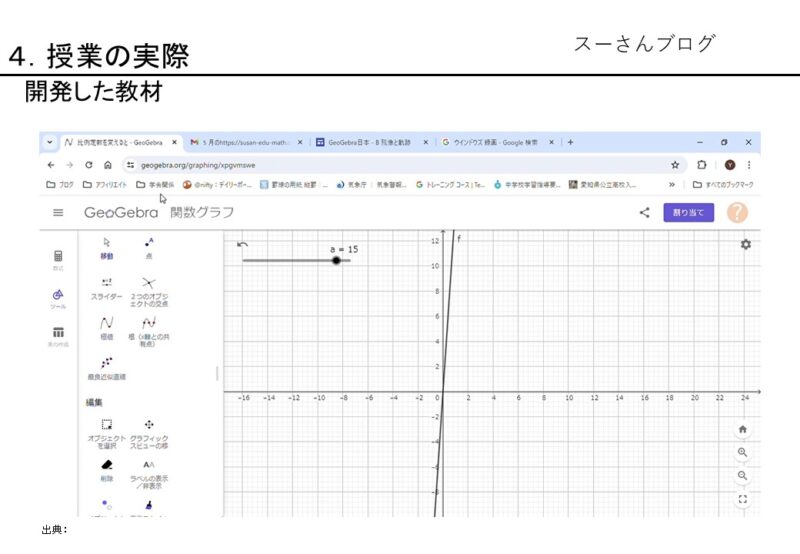
この教材【資料8】は、左上の「a=-0.5」と書かれているバーを左右に動かすと、比例定数の値0.5刻みで増減し、描かれるグラフ(本画像では「f:y=-0.5x」)がバーの変化に伴って連続的にかわる教材である。
【資料8】生徒Aがかいたグラフ
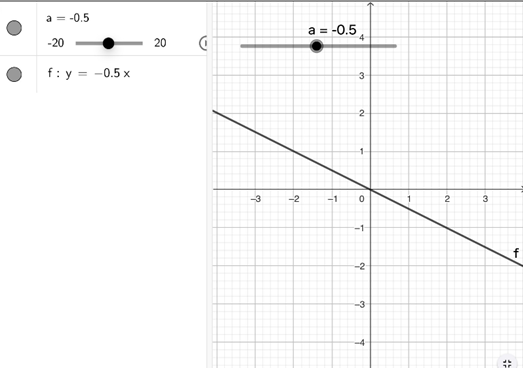
本時ではこの教材を生徒のタブレットに配付し、「前時では、比例のグラフの特徴をたくさんみなさん見つけてくれました。
ところで、生徒Bさんが、グラフをじーっと見ていたら、前の時間ではみんなが気づかなかった特徴を見つけてきてくれたよ。それをこの教材を使って見つけてみよう。」と話をした。
生徒Aは、aの値を増減させる中で、「グラフは原点を中心にぐるぐる回っている感じがする」ということを見つけることができた。
連続的にグラフの変化を追えるので、比例のグラフは原点を通ることを生徒Aが発見できたと考える。手だてⅢは有効に働いた。
さらに、生徒Aは【資料9】のような振り返りを書いた。
【資料9】生徒Aの振り返り

これは、「原点から次の点をとる時に、xを1増やして、yを比例定数分動かしたところに点を打てば、グラフがかける」という気づきである。
2年生の一次関数の傾きの概念そのものである。
ICTを活用したことで、実際にグラフをかく場合の数倍のグラフを見て考察することができたからこそ、できた発見である。
ここからも手だてⅢが有効に働いていることが覗える。
反比例のグラフの特徴を掴む生徒A(第12時)・・・手だてⅣ
本時は、$y=12/x$のグラフをかき、反比例のグラフの概形をつかむことをねらいとして授業を行った。
前時で、$y=12/x$の表を書いていたので、座標軸に点を打つ作業から始めた。
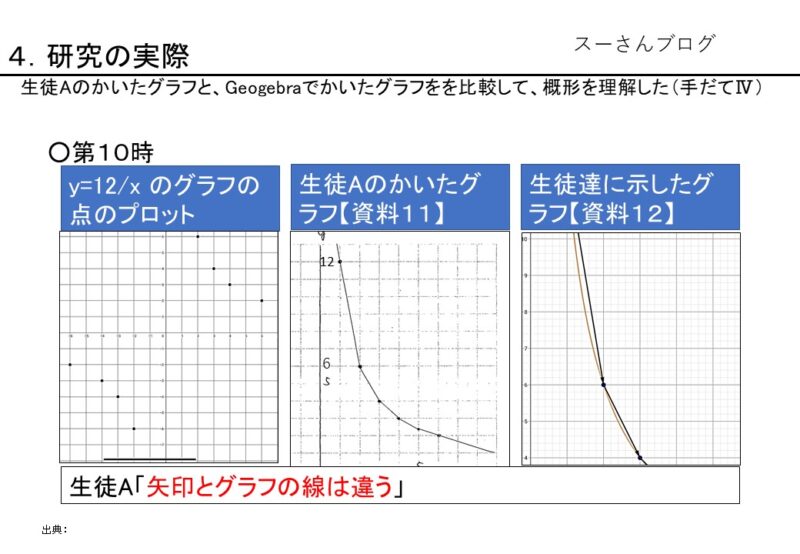
点を打った後【資料10】、「点を結んでグラフをかきましょう」と伝えた。
【資料10】$y=12/x$の点のプロット
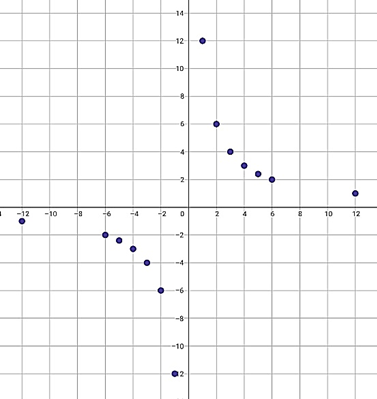
生徒Aはプロットした点と点の間を定規で直線になるように結び、lim(x→∞)、lim(x→0)の部分は直線をそのまま延長してかいた【資料11】。
【資料11】生徒Aのかいたグラフ(第1象現抜粋)
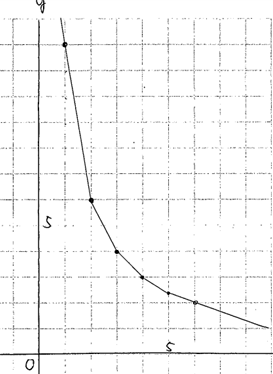
フリーハンドで点と点を結んでグラフをかいていた生徒もいたので、2つのグラフを取り上げ、「定規で結ぶのと、フリーハンドで結ぶのとでは反比例のグラフとしてどちらが正しいだろうか、タブレットで確認してみよう」と【資料12】を提示した。
【資料12】
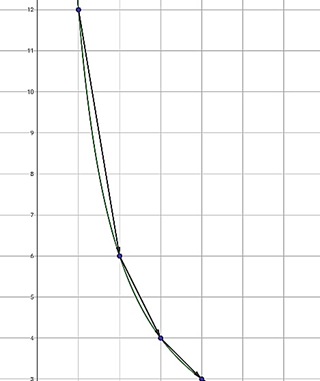
これを見て、生徒Aは「実際のグラフの線は曲がるんだ。僕は矢印の線の部分だと思ったけれど、実際には曲線になるんだね。」と気づき、つぶやいた。
さらに、「ずっとxの値を大きくしてグラフを伸ばしていくとどうなると思う?」と尋ねたところ、生徒Aは、「x軸を突き破って、x軸の下に線がいくと思う。」と回答をした。
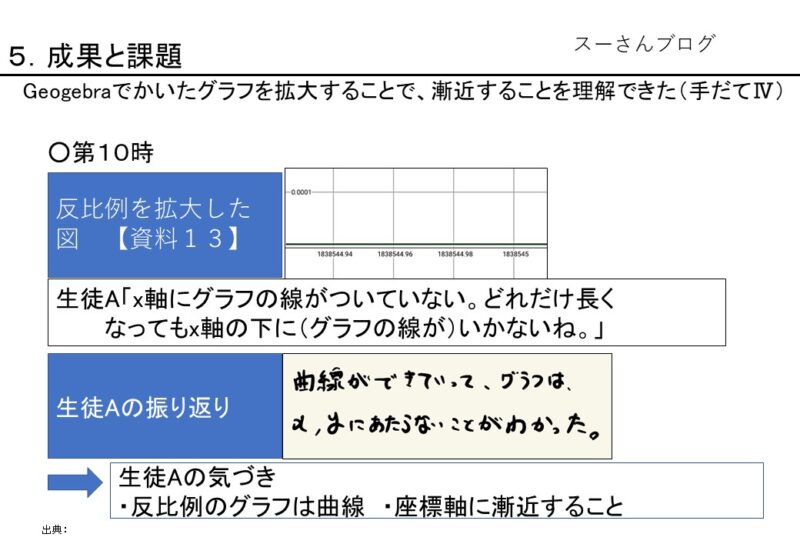
そこで、タブレットで、x=1838545あたりのグラフの様子【資料13】を見せたところ、生徒Aは「x軸にグラフの線がついていない。これ、どれだけ(xの値が)大きくなってもx軸の下に(グラフが)いくことはない。」と発言した。
【資料13】$y=12/x$のグラフの$x=1838545$における様子

そこで「12をどれだけ大きな数で割っても、0を下回ることはないね。」と表で教師と確認し、反比例のグラフ座標軸にグラフの線が漸近することを確認した。
生徒Aの振り返りは【資料14】である。ここから、生徒は「反比例のグラフは、曲線でできていること」、「反比例のグラフはx軸、y軸に漸近すること」を理解していることが分かる。
【資料14】第12時の生徒Aの振り返り
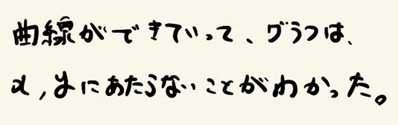
研究の成果と課題
手立てⅠについて
身近にあるもので関数表現できるもの(本研究では、水槽に水がたまる映像)を視聴させることで、関数の意味を獲得できるように試みた。
結果、生徒Aは、「時間がたつと、水が増える」と例示をすることができた。
振り返りにも「『○○が変わると、○○になる』ものが関数」と関数の意味理解を定義にそって、生徒Aなりにできていることが覗える。
手だてⅠは有効に働いた。
手立てⅡについて
本研究では、比例定数を生徒に決めさせ、グラフをノートに書くのではなく、「Geogebra関数」を使ってタブレット上にかかせることを試みた。
生徒Aは、まず4つのグラフをかいて観察し、「比例定数が大きくなればグラフが縦になる(傾きが急になる)」ことを見つけることができた。
また、他の生徒との意見交流の中で、自分のグラフと友達のグラフを対比させることで、「比例定数が小さくなればグラフが横になる(傾きがゆるやかになる)」ことを見つけられた。
生徒の実態でも述べたが、単元前では、比例の知識が少なかった生徒Aである。
それが、ICTを活用してグラフをかき出し、比例のグラフの特徴を見つけられたのは、タブレットは関数の式を入力すれば、正しいグラフかいてくれるという信頼からくると考えられる。
数学が苦手な生徒Aのような生徒にとって、ICTを活用することでグラフの特徴などを見つけるのに自信をもって取り組めることが分かった。
さらには、自分の考えと友達の考えを対比し、考えを深める姿も看取ることができた。
手だてⅡは有効に働いた。
手立てⅢについて
生徒Bの第8時の振り返りを基に、「比例のグラフは必ず原点を通る」ことに気づけるような教材を作成した。
グラフの変化を動的に見せる中で、比例定数の値がいずれでも必ず原点を通ることに生徒Aは気づくことができた。
逆に、前時のように散発的にグラフをかいていても原点を通ることをほとんどの生徒が気づくことはできていない。
ICTを活用し、動的にグラフをみせることことは、教科書では成しえなかった発見を促すことができるといえる。
手だてⅢは有効に働いた。
手だてⅣについて
反比例のグラフがどんな形になるか予想を立ててかき、その後タブレットで反比例のグラフを見せ、比べる活動を行った。
タブレット上では正確にグラフがかけるという性質を使って、グラフは曲線になることや、座標軸に漸近することを視覚的に理解することができた。
また、表を使ってxの値が限りなく大きくなっても、yの値は0にならないことを確認し、生徒Aは表とグラフを関わらせながら反比例のグラフの特徴について理解を深めることができた。
以上の生徒Aの姿から手だてⅣは有効に働いたと考える。
今後の課題
本研究で講じたICTを活用した手立ては、中学校2年生や3年生の「一次関数」や「二次関数」での学習でも活用できると考える。
本研究で得ることのできた知見を活かし、上記の2単元でも手立てを講じ、ICTを活用したときの生徒も学びについて今後研究を進めることとする。
参考文献
- 永田潤一郎(2022).「『365日の全授業』DX 中学校数学」.明治図書
発表スライド
愛知県数学教育会で実践報告をしてきました。









指導助言
愛知教育大学 石川雅章先生から、ご指導をいただけました。
意欲面で、生徒Aが数学の勉強に興味を持って授業をしていた、と書きましたが実際の理解につながっているかは微妙であるという指摘が…。
ごもっともです。逃げてしまった部分であります。
指導していただいたときのスライドをブログに掲載許可をいただいたので、掲載させていただきます。
20240821_三教研指導助言(鈴木先生)さらにブラッシュアップしていかなければと身の引き締まる思いです。
本大会の感想が石川先生のHPに上がっていました!
関連記事
研究を計画していたときの記事も書きました。
研究プロットと合わせて読んで、どういうふうに変わっていったか見ていただければと思います。
以前に書いた、比例分野の実践例です。ご覧ください。









コメント