【中2 数学 指導案 正多角形の内角の和 Scratch】正$5/2$角形を書こう

正n角形の内角の和、外角の和について理解をしたところで「正$5/2$角形を書こう」という問題を準備し、授業を行いました。

どんな授業になったか紹介します。

ねらい

・内角の公式、外角の公式を活用して、正（分数）角形の図形を書くことができる。

授業の実際

正 $5/2$ 角形を書こう。どんな図形になるかな？

多角形の内角の和の公式　「多角形ｎにおいて多角形の内角の和は$180°\times (n-2)$で表せる」ことを復習したあと、

「正$5/2$角形を書こう。どんな図形になるかな？」と発問し、早速取り掛からせました。

生徒は、なんじゃそりゃと戸惑いながら、問題に取り掛かっていました。

内角が何度になるかわからないので、内角の和の公式に当てはめ、

$$180°\times (5/2-2)＝180°\times 1/2=90°$$

このように、正$5/2$角形の内角の和を求めました。

したがって、一つの角の大きさは

$90\times 5/2=36°$

となります。

3本ほど辺を引いてみると、こんな感じになります。

子どもは書けないよ！というのですが、それでも根気強く書いた子どもは次のような図形になることに気づきました。

これを「星型多角形」といいます。

さて、他に星型多角形になるのは、nがいくつのときでしょうか？

また、星型多角形において、外角に規則性がはあるのでしょうか？

星型多角形になるのは、nがいくつのとき？

このときに、いろいろ計算させて確かめるのも一つですが、プログラムを組んで、試行錯誤させてみるのはどうでしょうか？

今回は以下のページのScratchを使っていろいろ試行錯誤させてみました。

Check out what I made

I wrote the code myself with Code.org

studio.code.org

1つの内角が、26°のとき

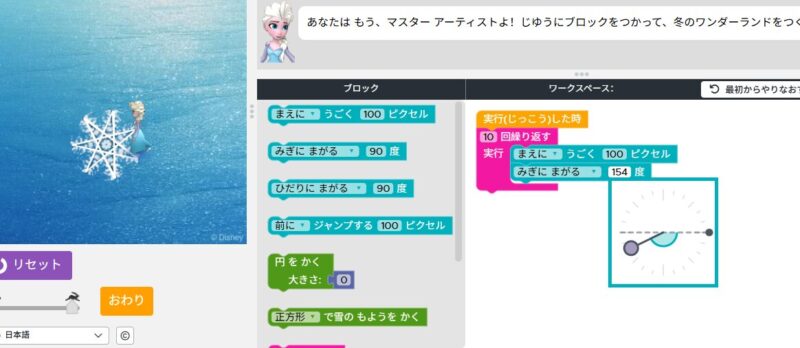
うまくいきました。

これは失敗した例ですが、79°だとこんな感じ。これは星型多角形には帰着できませんでした。

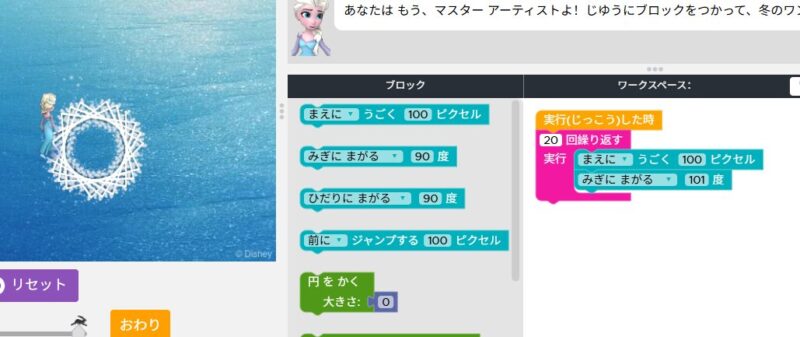
スピログラフで書いたような図形ができあがりました。

さて、うまく星型の多角形が出来上がるときは、n角形のnをどのように設定すればよいのでしょうか？

最後に

参考にした文献では、いくつか綺麗にできるｎを提示して、そこからどんな法則があるのか見つけるような授業を作っていました。

プログラミングを使えば、簡単に試してみることができるのが大きなメリットです。

外角と内角を変換するひと手間（わからない人は、実際にプログラムを組んでみましょう）がありますが、その中で新しい発見も得られると思います。

一度ためしてみるのはどうでしょうか？

参考文献

参考HP

https://www.chikyo.co.jp/m/pdf/free05.pdf

アナと雪の女王 – Answer to HourofCode

hourofcode.info