平方根の最後では、「平方根の利用」として、ピザの問題が扱われます。
この問題って、実は、今後の学習の導入材料として、色々示唆深い問題ではないかと常々考えています。
皆さんこの問題を読んでどう指導していますか?
問題

「ピザを作ろう」
けいたさんは、半径10cmの円形のピザを食べました。量が足りなかったので、もっと大きなピザを食べたいと思いました。
別の日に、面積が前回の2倍のピザを作ろうと思いましたが、半径を何cmにすればよいかわかりませんでした。
(話し合おう)円の半径を2倍にすると、面積も2倍になるのでしょうか?
ー啓林館.「未来へ広がる数学3」.P61
さて、この問題の面白いところが「直感に反する」ところです。
読者の方ならご存知の通り、半径を2倍にすると、面積は4倍になります。
子供達は、実際に計算をしてみて、半径を2倍にすると、面積は4倍になることを確かめます。
子どもは結構びっくりします。
実際に図形を書いてみても、半径を2倍にすると、面積は2倍より大きくなることが直感的にわかります。
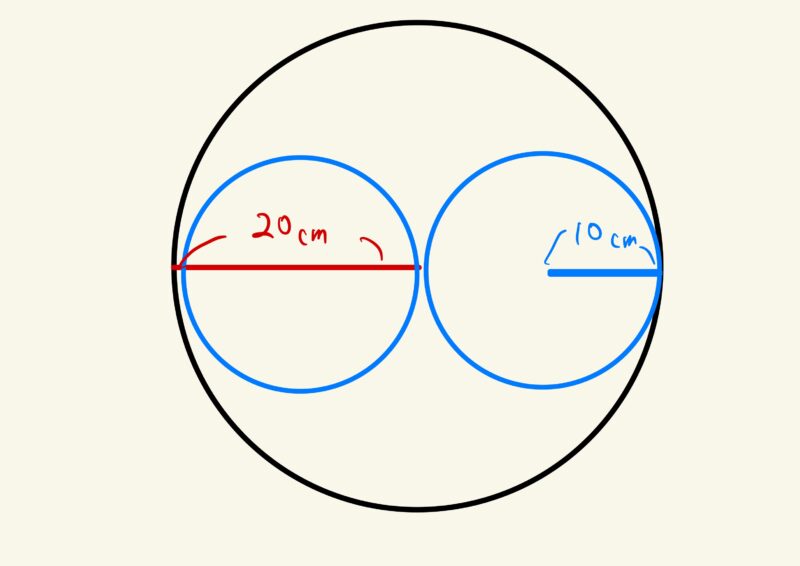
半径を何cmにすればいいのかな?
生徒たちの次の問いとして「半径を何cmにすればいいのかな?」が出てきます。
ここで、生徒は、まず半径10cmの円の面積を考えます。
$$10×10×π=100π$$
従って、面積2倍のピザの面積は200π㎠となります。
そうすると、面積2倍のピザの半径は・・・と求めていきます。
問題の発展可能性

この問題は以下の2つの問題を投げかけます。
- 二次方程式の必要性
- 相似な図形の面積比
一つずつ見ていきましょう。
二次方程式の必要性
さて、先ほどは、二次方程式という言葉を出さずに、問題を解こうとして問題を書いています。
しかし、このような解き方をする子もいます。
面積2倍のピザの半径をrとすると、
$$π×r^2 = 200π$$
$$r^2 = 200$$
「あれ、文字が2乗の方程式が出てきたぞ。これはどう解けばいいのかな?」と自然に二次方程式が目の前に現れるのです。
もちろん、「方程式の意味を考えれば、『2乗したら200になる数は何だろう?』という意味の方程式だよね」と確認すれば、答えを導き出すことができる生徒も出てくると思います。
けれど、「これって、今までの方程式と何が違う?」と全体で取り上げ尋ねることで、すんなりと、次章の「二次方程式」と必要性が生徒に理解できるわけです。
半径は、方程式を使わなくても解けることをおさえつつ、方程式の考えが出てきた場合は、「$r^2 = 200$はどう解いていけばいいのか、次から考えよう。」と授業では押さえるようにしています。
相似な図形の面積比
知っている教師の立場からすれば、今回取り扱う二つの円は相似なので、面積比と半径の関係を知っていれば解くことはできます。
これは、後に中学校3年の「相似な図形」で学習を進めていくのですが、その初歩的な問題という位置付けで見ることも可能です。
この時間では、取り上げる必要は全くありませんが、「相似な図形」で相似比の学習をした際に、「実は、この学習は、以前にやったことがあるんだよ・・・。」と生徒に投げかけることで、平方根で学習したことと、相似な図形の学習が地続きになっていることが生徒は気づくはずです。
最後に

今回は、教材研究的に、平方根で取り扱う「ピザ」の問題から、どんな学習に発展するのかを考えてみました。
数学は、系統建てられた教科です。
よく、「平方根」を学ぶには、「今までどんな学習があるのか」を調べますが、「平方根」がどの分野に発展していくかはあまり考えません。
特に単元ごとにみていくのではなく、問題単位でどの分野に発展して行くかは、ほとんど考えることがないでしょう。
教科書の朱書きでも紹介されていることは少ないです。
この問題は、どんな意味を持ち、どのように発展していくかと見ていくことで、指導者の指導力も伸びてくると思いますがいかがでしょうか?
皆さんの感想、コメントをお待ちしています。

このあと、丸太の問題を解いていきます。そこについての記事はこちらをご覧ください。
平方根の指導案を他にも書いています。合わせてご覧ください。







コメント