何回も正の数・負の数の除法の授業をしているのですが、今回面白い誤答が出てきました。
しかも一人ではなく、複数人。
もしみなさんは、以下のような誤答がでてきたらどうしますか?
生徒の反応について、今回は記事にします。
授業の様子

まずは、2つの問題を提示して取り組みました。

$6÷2=3$
$-6÷2=-3$
この2つは、小学校で勉強した「わり算の考え方」で「6を2つに分ける」「-6を2つに分ける」という考えで、子どもたちはすんなり答えに納得しました。
次に$6÷(-2)$を取り扱いました。
ここで、クラスの生徒5、6人は、「12」と商を出してきました。
しかもその生徒は数学の成績は良い生徒です。
なぜ、そう考えたと思いますか?
考えた生徒は「(-2)を割るということは、”ー”は言葉の意味を反対にするので、”2をかける”ということになる。だから$6÷(-2)=6×2=12$」とノートに理由を書きました。
みなさんはここで、どう反応しますか?
今回の授業では、複数この考えをした生徒がいたので、あえて最初に全体の場で取り扱いました。
この誤答から、逆数をかけるという反論をする生徒がいると考えたからです。
予想通り「逆は逆でも、逆数をかけると思う。小学校でやったじゃん。」と発言をしてきました。
つまり、計算方法は以下の通りになります。

逆数に計算については、教科書だと、後に学習します。厳密な証明はしないので、「お、小学校の学習を使えたね!」と価値づけました。
ただ、これではどちらが正しいか判断できません。
そこで、「もう一つ別の方法で答えを導き出して、答えが一致したらいいよね。なにか方法ある?」と問い直しました。
生徒からは出てこなかったので、割り算の確かめ算を使った方法を紹介して確認をしました。
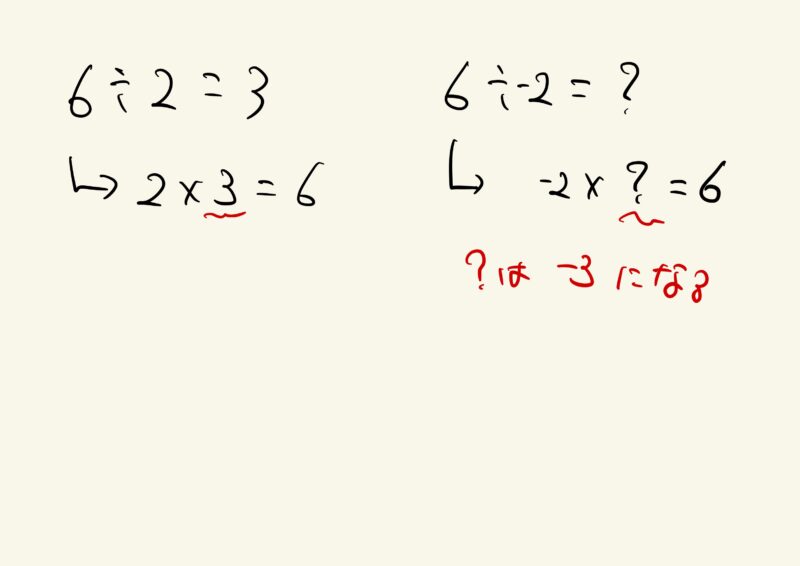
2つの方法で答えが(-3)と導き出せたので、答えは「−3」と決着しました。
このあと「$(−6)÷(−2)$を考えよう」と話を進めました。
「今、使った考えを使って説明できるかな?」と理由もつけて考えをまとめる用意進めました。
逆数で進めた生徒と、確かめ算の方法で進めた生徒、半々くらいでした。
最後に
負の数の除法は、乗法になるという考えは今まで見たことがありませんでした。
けれど、今ままでの計算は、$3ー(−2)=3+2$のように、マイナスがプラスになりました。
減法が加法に変わったと見ているのです。
だから、本時の誤答も理解できます。
逆に今まで出てこなかったことも、教材研究としてこの誤答を想定できなかったことが悔しいですし、授業の面白いところだなと思っています。
こういう誤答をうまくキャッチしつつ、数学の世界を広げていけると面白いなと感じた授業でした。
正の数・負の数の計算場面の授業は、こちらにも記事にしてあります。合わせてご覧ください。

「正の数・負の数の単元」の別の授業記録記事は以下のリンクをご覧ください!








コメント