今回は、中3の「式の展開・因数分解の利用」において、生徒がどんどん考えを広げていったのが面白かったので、様子を紹介します。
問題

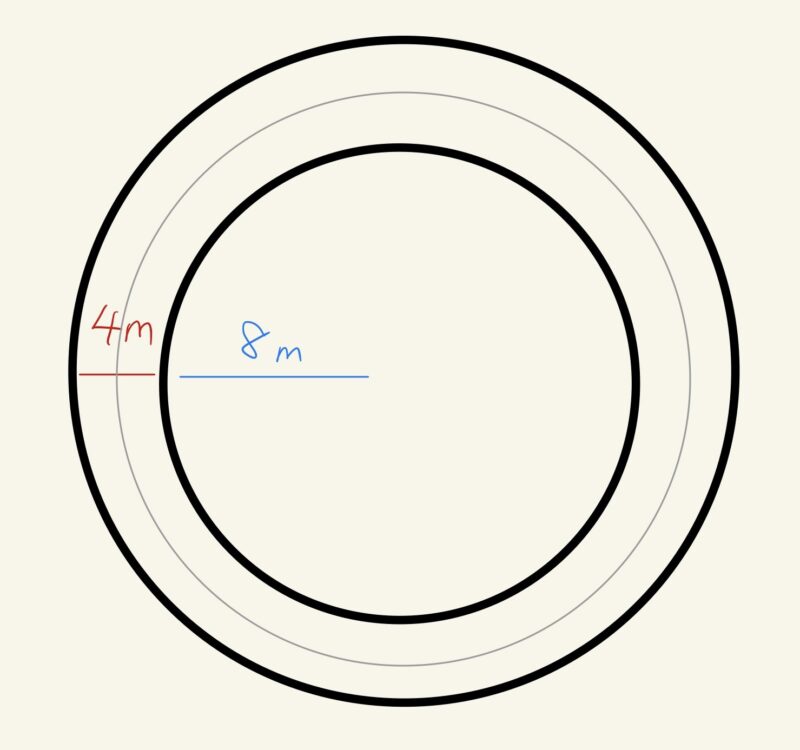
半径8mの円形の花壇の周りに、図のように幅4mの道がついています。
道の面積と道の真ん中を通る円周の長さと道幅の積をそれぞれ計算して比べてみましょう。
「未来へひろがる数学3」P31.(2021).啓林館
実際の数値で、
$(道の面積)=(道の真ん中を通る円周の長さ)×(道幅)$
と確認をします。
そして、実際に数値が文字に変わって以下のような証明問題が出題されます。
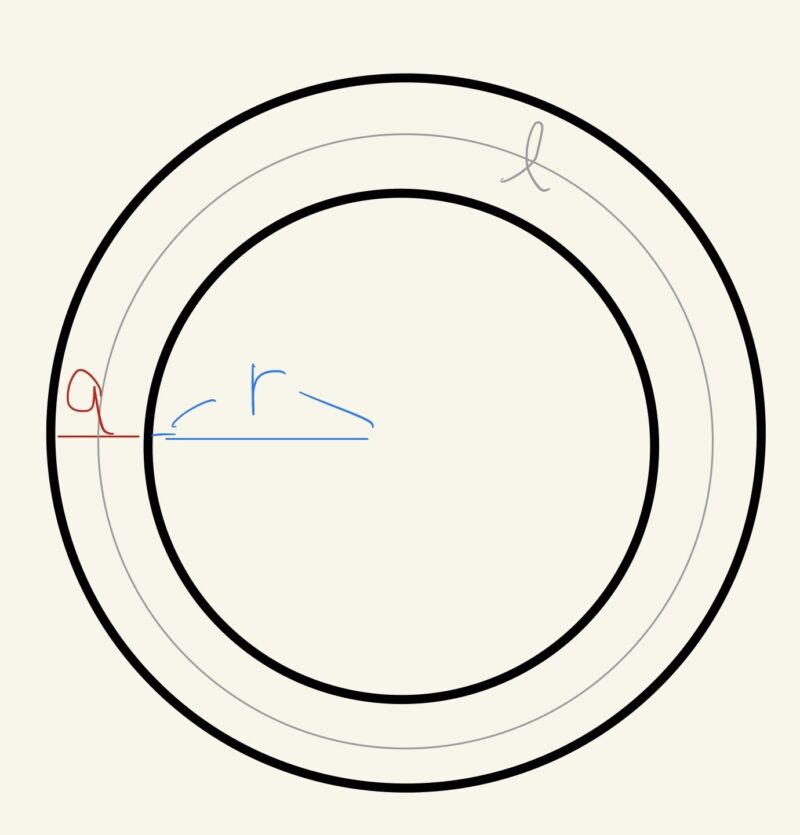
半径$r$の円形の花壇のまわりに、下図のように幅$a$の道がついています。
この道の面積を$S$、道の真ん中を通る円周の長さを$l$とするとき、
$$S=al$$
となることを証明しなさい。
「未来へひろがる数学3」P32.(2021).啓林館
この問題を取り扱いました。
解法にたどり着くまでは、以前の記事と同じ流れです。こちらをご覧ください。
この問題の発展

この問題を解いた後、演習問題で円の形が、正方形になった場合、長方形になった場合でも、
$(道の面積)=(道の真ん中を通る図形の周の長さ)×(道幅)$
が求めることができるかを証明していきます。(実際に求めることは可能です。)
ここで生徒から「いろんな図形で今回紹介された式が使えることはわかった。けれど、従来の(図形全体の面積)ー(真ん中の図形の面積)で面積を求めた方が楽・・・。」
ということをみんな言っていました。
「そうだよねー」と話していたところ、こんなことを言い出す子がいました。
「公園の池の周りに道を作るときは、図形そのものがぐにゃぐにゃしているじゃん。でも、道の真ん中をコロコロ(ウォーキングメジャー)で測れば、実際の面積を求められるから、使えるんじゃない?」
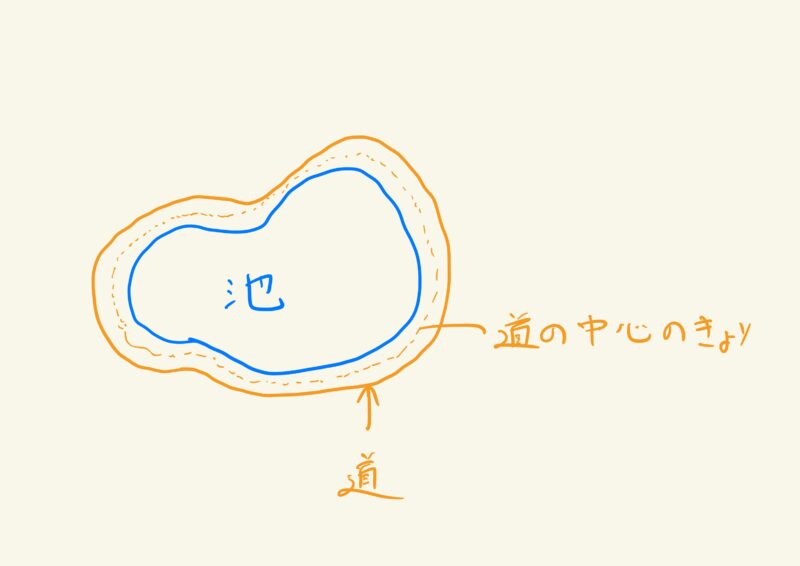
「でも、道幅一定とは限らないじゃん。途中で道幅を変える場合も、この公式が使えるの?」
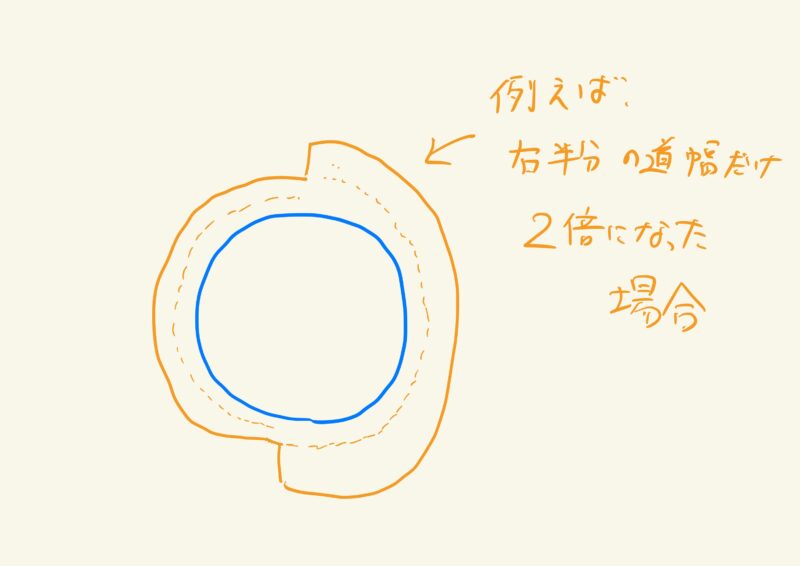
という話。
さらには、「体積に拡張した時も同じ公式が使えるかな?
つまり、ドーナッツを想像して
($(ドーナッツの体積)=(ドーナッツの生地の部分の中心を通る周の長さ)×(ドーナッツの生地の部分の断面積)$)で、ドーナッツの体積を求められるかな?」

こんな疑問が湧いてきました。
これこそ、「数学的見方を使って考えを広げる」生徒の姿ですよね。
授業では取り扱えませんでしたが、数学の探究テーマとしては面白いテーマです。
本校では、朝の学習の時間に「探究の時間」を設定し、夏休みの自由研究みたいなことを行なっています。
この時間で扱っていきたいなと思いました。「探究の時間」については以下の記事をご覧ください。
実際に確認することができたらこの記事で紹介しますね。
最後に

池の話のように曲線で囲まれた面積についての証明は、高校の積分の知識が入りそうです。
ただ、実際のグラウンドに絵を描いてみて実測してみて確認をするという方法をしてみてもいいかも知れません。
体積はもしかしたら中学校の知識だけで解くことができるやも知れません。
ドーナッツ形だと厳しいので、球の体積だったらいけるのでしょうか?
このように条件設定を厳しめにして始めて一般化をしていくことで、色々考える余地が出てきそうです。
生徒と一緒に探究をしていきたいと思います。
今は、インターネット、生成AIもあり、学びを自分で広げていくことも簡単になってきています。
その目を育てていきたいなと思っています。
みなさんの授業でこの場面はどう取り扱っていますか?
ぜひ教えてください。

中学校3年生 式の展開・因数分解の授業案の記事を合わせてご覧ください。









コメント