今日は、中3 式の展開・因数分解の利用の部分の授業です。
子どもの式の見方って素晴らしいなと感じたので、今回記録に残したいと思います。
展開・因数分解の他の授業案はこちら!
問題
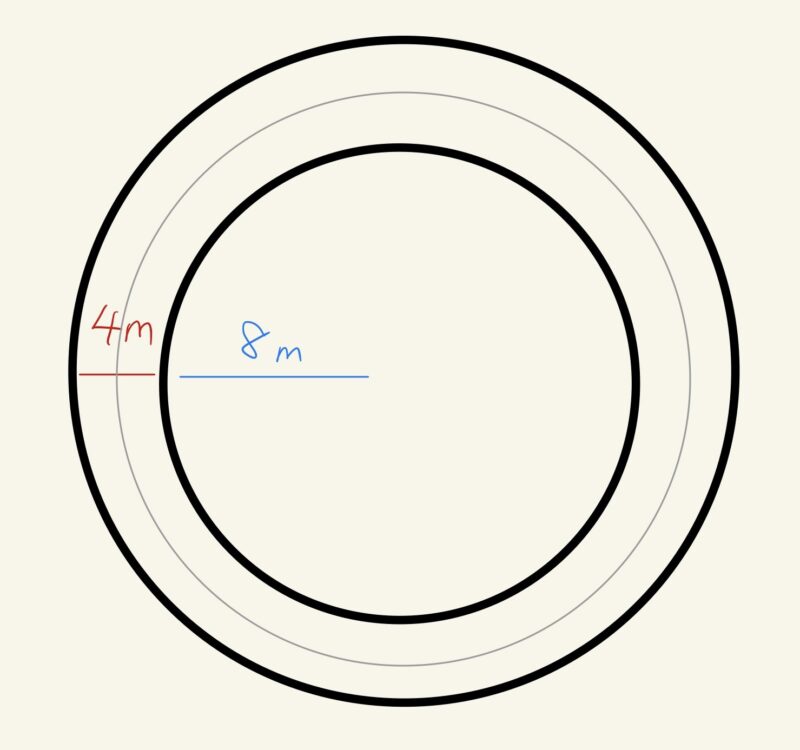
半径8mの円形の花壇の周りに、図のように幅4mの道がついています。
道の面積と道の真ん中を通る円周の長さと道幅の積をそれぞれ計算して比べてみましょう。
「未来へひろがる数学3」P31.(2021).啓林館
実際の数値で、
$(道の面積)=(道の真ん中を通る円周の長さ)×(道幅)$
と確認をします。
そして、実際に数値が文字に変わって以下のような証明問題が出題されます。
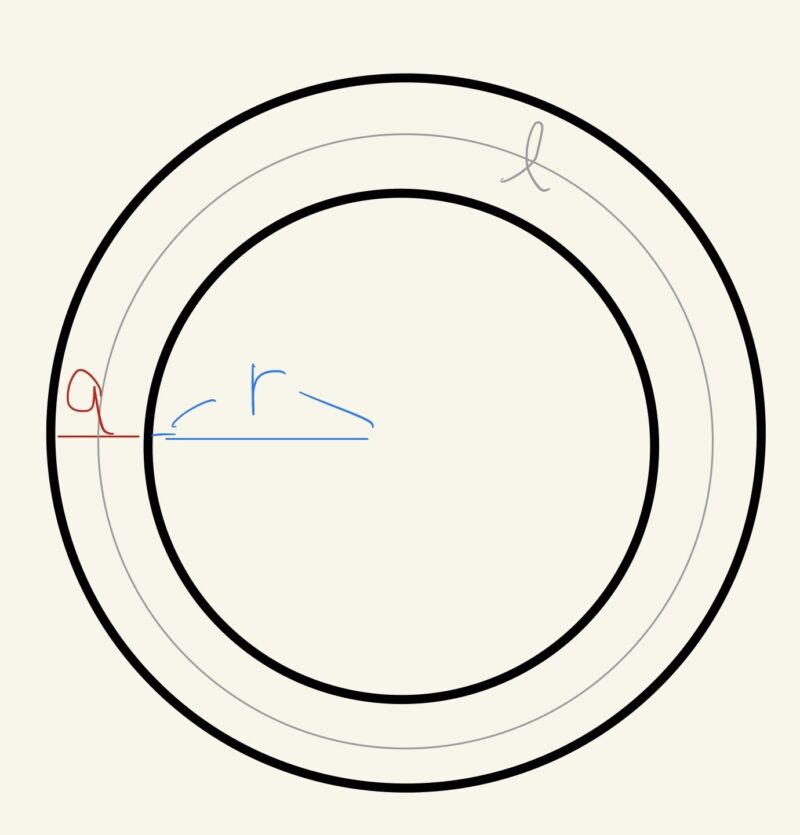
半径$r$の円形の花壇のまわりに、下図のように幅$a$の道がついています。
この道の面積を$S$、道の真ん中を通る円周の長さを$l$とするとき、
$$S=al$$
となることを証明しなさい。
「未来へひろがる数学3」P32.(2021).啓林館
板書
生徒の解答
以下のように子どもたちは考えました。

―① の部分。
$S$を求めた際に
$πa^2+2πar=πa(a+2r)$
と因数分解しています。
これは、こちらが意図したわけではありません。$S$を求めた後、
「次、何をしよう?(教師は、$al$を求めると言ってほしい)」
と尋ねたときに、
「因数分解する」
と子どもが言ったのです。
その意見を、そのまま受けて、子どもたちの次の意見を待っていました。
この式をずっと眺めていると、ある子どもが、
「$πa(a+2r)$の$π(a+2r)$って、そのまま$l$を表しているんじゃないか」
と話しだしました。
「どういうこと?」
って尋ねると、
「$l$の直径は図から$2r+a$だから…」
と説明を始めました。
そこから、図で実際に$l$の円周を導き出し、$S=al$であることを確認しています。
教科書では
教科書では、$S$も$al$も展開して、計算結果が同じだよねということを確認して、証明を終了しています。
ただ$S$を求めたときに、因数分解というひと手間を加えることで、直感的に$S=al$が見えてくるんですね。
子どもたちの観察はすごいと思った授業でした。(教材研究不足)
まとめ
因数分解というひと手間を加えることで、直感的に分かる式へと変貌をとげました。
エレガントな数学的な見方というのは、子どもの中に隠れているんだなと私が勉強になった授業でした。
みんなすごい!






コメント