今回は、小4 小数の単元で行った実践を公開します。
使用した教材は教科書を準拠しつつ、トランプゲームを用いて思考を促したりと工夫しました。
特に子どもがそれぞれの考えの違いに気づき、学習を深めることができるだろうと
仮説を立てて、手だてを講じました。
ぜひ、ご意見ください。
主題設定の理由
児童の実態
略
平成３１年度全国学力・学習状況調査から考える主体的・対話的な児童の姿と，本研究における２つの「ずれ」の定義
「平成３１年度全国学力・学習状況調査算数 問題３」【資料１】を見てみる。
【資料１】平成３１年度全国学力状況調査 算数 問題３の一部
【資料１】平成３１年度全国学力状況調査 算数 問題３の一部この問題は，ともやさんの計算の仕方と，ゆいなさんが解き方を解釈した文を読み，その後，児童が類題を解く形式になっている。
この問題形式の流れは，この年の算数のどの問題にも共通している。
ここから，授業の対話の場面で，「友達の考えを聞き，その考えを解釈し，別の場面で活用していく場」を設定することが求められていることが分かる。
そこで，友達の発言を自分の言葉で言い直したり，友達や，教師が提示した考えと自分の考えを比べる場面を設けたりすることを考えた。
そうすることで，「あの子の言ったこと分かる。こういう意味だよね。」，「自分と考えが違うな，どこが違うのかな。」と考え，個々の児童の「思考のずれ」が現れてくる。
このずれを学級全体で明らかにしていく中で，対話的に学ぶ児童の姿が現れると考えた。
さらに，友達の意見について考えられるようになるには，自分の考えをもつことが大切である。
そこで既習事項と本時の学習を比べれば，「既習事項とのずれ」が明確になる。
そこから，本時の課題を具体化し，課題の解決に向けて自分の考えがもてるので，主体的に学習に関われるだろうと考えた。
本学級の児童の姿と，全国学力・学習状況調査を踏まえ，「既習事項とのずれ」，「思考のずれ」を児童が意識できるようにし，主体的で対話的で深い学びになるよう本研究の主題を設定した。
研究の構想
目指す児童の姿
「既習事項とのずれ」に気付き，課題をつかみ，主体的に学習する児童。
友達との「思考のずれ」に気付き，対話的に課題を解決する児童。
研究の仮説
Ⅰ「既習事項とのずれ」に気付けるように課題をつかませることで，児童たちは，本時の課題を明確につかみ，主体的に活動するだろう。
Ⅱ 友達や教師の提示した考えの「思考のずれ」に気付けるように意見をとりあげることで，児童たちは，対話を通して学びを深めるだろう。
研究の手立て
Ⅰ ①新たな問題と既習事項を比較できるように，本時と既習の問題を並べて提示し，何が違うか尋ねる。
②新たな問題と既習事項を比較できるように，これまでの学習の足跡を掲示し，既習を振り返る場面を設定する。
Ⅱ ①友達との「思考のずれ」が明確になるように，対話の場面で友達の意見を，自分の言葉で言い直すように働きかける。
②友達との「思考のずれ」が明確になるように，対話の場面で出てきた考えと自分の考えを比べるように促し，どうして違うか尋ねる。
授業の実践と考察
1.5Lのぺットボトルをいっぱいまで水を入れると，かさはどれだけになるかな？（第１時）
単元を貫く課題への気付き【手だてⅡ－①，手だてⅠ－①】
まず，1.5Lのペットボトルを児童に提示し，「このペットボトルには，どれだけジュースが入っているだろうか。」と尋ねた【資料２左側】。
【資料２】提示したペットボトル児童たちから，すぐに「1.5Ｌ」と答えが返ってきた。ここで，1Ｌマスの図【資料３】を提示し，「このマスに，水を入れると，どれだけになるか色を塗ってみて。」と指示した。
【資料３】１Ｌますの板書正答が出たところで，教師は「なぜこれで正解なの？」と抽出児Aに尋ねた。
抽出児Aは，「1.5Ｌだから，1Ｌと0.5Ｌ。0.5Ｌは，1Ｌの半分だけぬればいい。」と答えた。
これでは，まだ1Ｌを10個に分けて0.1Ｌという本時で必要な既習事項が押さえられていないと考え，「半分ってどういうこと？」と全体に尋ねた。
児童Bが「一目盛りは1Ｌを10個に分けているから0.1Ｌ。だから，(0.1Ｌが)5つ分で0.5Ｌだよ。」と答えた。もう一度，本当かどうかクラス全体に尋ねると，一様にうなずいた。
次に，【資料２ 右側】のペットボトルを提示した。
そして，「ペットボトルの水を継ぎ足しました。量を調べたら，【資料３】のようになったよ。」と話すと，抽出児Aは「ちょっきりじゃない！」と1.5Ｌの時とは違うことに気付いた【資料４黄色下線部】。
抽出児A：ちょっきりじゃない！
児童C：変！
Ｔ：Aさん，ちょっきりじゃないって言ったね。Cさんも変って言ったね。Cさん，Aさんの言ったこと分かる？
児童C：いままで，（1Ｌますの）線の上にきていたでしょ。ちょっきり何Ｌっていえたけど，今回は，線と線の間になっている。ちょっきりじゃなくって，何Ｌか分からない。
Ｔ：Aさん，そういうこと？
抽出児A：（うなづく）
児童D：たしかに，ちょっきりじゃなくて，どうすればいいか困った…。
【資料４】児童が課題を意識するまで
この「ちょっきり」の意味をほかの児童に解釈させることで，抽出児Aの気付いた「既習事項とのずれ」が明らかになり，課題を明確にできるだろうと考えた。そこで，同じように「変。」と言った児童Cに「Aさんの言ったこと分かる？」と尋ねると，「いままで，（1Ｌますの）線の上にきていたでしょ。ちょっきり何Ｌっていえたけど，今回は，線と線の間になっている。ちょっきりじゃなくって，何Ｌか分からない。」と話した【資料４赤色下線部】。
児童Dも，「たしかに。」と理解を示しながら，困ったことに同意した。抽出児Aのつぶやきを児童Cの言葉で説明させたことで，今まで習ってきた小数第１位までの小数では表現できないことに児童Dも気付き，思考のずれが明確にし，課題を作りあげることができた。
手立てⅡ－①は有効に働いた。また，既習の問題と新しい問題を並べて提示したことで何が違うか見つけ，課題を明確にできた。手立てⅠ－①も有効に働いた。
0.01の意味理解と抽出児Aの学習の理解【手だてⅡ－①】
ここで，「ちょっきりじゃない，水のかさの表し方を考えよう。」と課題を板書し，考える時間をとった。
「同じように10個に分ければいいのに。」と書いた児童Eの発言を取り上げれば，1/100の位の存在に他の児童が気付くだろうと考えた。
児童Eが２回説明すると，抽出児Aは，「さっきと同じように」と，１．５Lの問題の考えを使って，さらに0.01の発見をした【資料５点線部】。
T ：みんな分かった？もう１回Eさん言ってくれる？
児童E：だから，1.5Lのとき１Lを10個に分けたでしょ。同じようにちょっきりになっていないところを細かく10個に分けてあげればいいの。
抽出児A：ああっ！
T：Aさん，ちょっと黒板でEさんの言ったことを教えて。
抽出児A：さっき，1Lを10個に分けて0.1Lが５個だったでしょ。今回は（ちょっきりじゃない部分を）さっきと同じように細かく分けて，細かく分けたのが８つ。だから1.58Lだよ。
児童F：さらに細かくすればいいんだ。
T：EさんやAさんが見つけた，この0.1を１０個に分けた１つ分を0.01Lといいます。よく見つけたね。
【資料５】0.01を見つけるまで
また，児童Eの発言の前では，児童Fは考えをもつことはできていなかった。
それが，児童Eの言葉を抽出児Aに言い直させたことで，0.01Lの発見を児童Fが「さらに細かくすればいいんだ。」と，0.01の意味を理解し，発見をすることができ学びを深めることができた【資料５黄色下線部】。
抽出児Aや児童Fの姿から手立てⅡ－①は有効に働いたといえる。
最後に，一の位から1/100の位まである位取り板を使って，1.58の数の構成を確認した【資料６】。
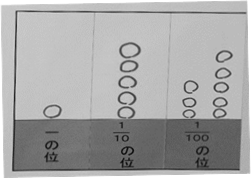【資料６】位取り板 抽出児A位取り板の様子から，抽出児Aは1.58の数の構成をきちんと理解していることが分かる。
また，抽出児Aは，「ちょっきりじゃないところが難しかったです。」と，ふり返りを書いた。
詳しく尋ねると「Eさんの10個に分けるで分かったよ。0.1を10個に分けていけばいいんだね。」と話した。位取り板【資料６】とふり返り【資料７】から，抽出児Aが本時の内容を確実につかんでいることが改めて分かった。
2.583を0.001だけを使って表そう（第４時）
本時の課題のつかむまで【手だてⅠ―①】
授業の最初に，「2.583は1, 0.1 , 0.01 ,0.001をそれぞれ何個集めた数か」を復習で尋ねた。
その後，本時の問題である「2.583は 0.001を何こ集めた数でしょう」と板書をした。「さっきと何が違う？」と尋ねると，抽出児Aは「0.001しか使ってはいけないんだね。けど，できるかなあ。」と発言した。
本時の課題になる「0.001しか使わずに小数を表すにはどうすればよいか」を抽出児Aが気付き，全員が共通認識することができた。
そして，全児童が，「2583個」と答えにたどり着いた。
既習と本時の問題を並べて提示し，違いを明確にしたことで，「2.583は0.001がいくつか」という課題をクラス全体でつかみ，学習活動に取り組むことができた。手立てⅠ－①は有効に働いた。
既習事項と比較して，考えた答えは正しいか説明しよう【手だてⅠ―②，Ⅱ―①】
このとき，なぜ2583個が正しいかは「小数点を消せば答えになる」という結果から観測した意見しか出てこなかった。
ここで考える時間をとると，児童Cは，「3のところを一の位と見れば，2583だよ。」と発言した【資料８】。
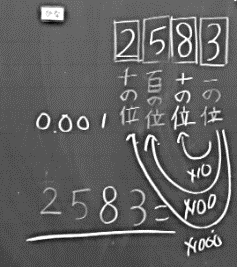【資料８】児童Cの板書これは，0.001を最小単位としてみて，位の関係を意識した説明である。
まだ，他の児童は理解ができない様子だった。
そこで，前時の学習【資料９，１０】を見れば，児童たちは理解できるだろうと考え，「Cさんが言ったことって，今までの勉強とつながっていないかな？」と尋ねた。
【資料９】第３時の学習の足跡
【資料１０】整数と小数の位取りの関係の見方（第３時の板書の写真）すると，児童全員が模造紙を見て，今までの学習とつながっているところを探し始めた。児童Cの発言と教師の指示から，既習事項とのつながりがないかと主体的に動き出している。
手立てⅠ－②はここで有効に働いた。
模造紙を見つめる中で，抽出児Aが「Cさんが言いたいこと分かった。」とつぶやいた。
抽出児Aは「これ（【資料９】）を見て。0.001が1000個集まると，1になるでしょ。
だから，Cさんは，ここ（【資料８】）の一の位を千の位って書いたの。
だから，（一の位の）2は0.001が2000個。0.5は500個，0.08は80個。だから合わせて2583個だよ。」と発言した。
さらに児童Fは「CさんとAさんの付け足しで，例えば，2583は1が2583個集まった数でしょ。同じようにあの（【資料１０】）の位の関係を見て，今回は0.001がいくつだから，0.001を1としてみれば，（小数も整数も４桁で）位の間が３つ空いているから，2583と2.583は同じように見ていいんだよ。」と話した。
この２つの意見から全員から「おぉっ。」という声が出た。
これは，整数の最小単位1をいくつと見るかの考え方と，本時の課題の0.001を最小単位としていくつかという考え方を統合して見た結果である。
児童Cの意見の意味をクラス全員で考え，抽出児Aと児童Fが話をつなげていくことで，学びを深めることができた。手立てⅡ－①は有効に働いた。
じゃんけんゲームをしよう（第５時）
位が上がったり，下がったりするのはなぜ【手だてⅡ－①，Ⅱ－②】
本時は「9.876を電卓に入れて，勝ったら×10，負けたら÷10をしよう。エラーがでたらおしまい」という活動をした。
小数を電卓で10倍，1/10するなかで，各位の数字の位がどう変わるかを児童は考えるだろうと考えたからである。
まず，前時の復習として，「9.876は0.001が9876個集まった数。」ということを確認した。
その後，電卓ゲームを行うと，児童はいくつかのことに気付いた【資料１１】。
【資料１１】第５時の気付きここで，「でも，なんで位が上がったり下がったりするんだろう。9.876を10倍した場合で考えてみよう。」と問い直した。
この問いに対して，「0.01が9876個」（0.001を単位量とした考え方）と「0.001が98760個」（個数に注目した考え）の２つの考えが出た【資料１２】。
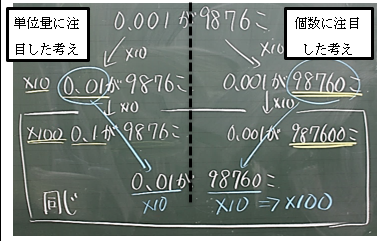【資料１２】位が上がる仕組みのまとめそこからの対話記録が【資料１３】である。「結局，0.001か小数の個数どちらかを，10倍，100倍しているから，桁が上がるんだ。」と，すべての解答のよさを認めながら，位が上がることを児童Cは気付いた【資料１３黄色下線部】。
児童B：0.01が0.001と比べて10倍していでしょ。0.1は0.001を10倍10倍で100倍。2桁上がることになるよ。
T：Aさんそれでいいかな？
抽出児A：うんT：じゃぁ，右の考えはどういうこと？
抽出児A：あ，分かった。0.001の個数が，9876個から98760個になって10倍。だから位が上がる。
T：じゃあ，100倍になると？
抽出児A：0.001が987600個。
T：個数が100倍しているから2桁あがるんだね。
児童C：結局，0.001か小数の個数のどちらかを10倍，100倍しているから，桁が上がるんだ。
【資料１３】位が上がる仕組みの追究
２つの面から解答を取り扱い，何が原因で位が上がるかを自分たちの言葉で言い直しながら，対話的に追究することができた。
手立てⅡ－①，②は有効に働いたといえる。
大きさくらべゲーム（第６時）
どうして，９が出ると負けになるのかな。【手だてⅠ－②】
本時は小数の大小比較の方法に気付かせるために【資料１４】のようなゲームを行った。ゲームをしていく中で，数の比べ方に目を向けさせたいと考えた。
２.自分の空いている場所，好きなところにカードを置く。
３.交互にカードを３回ずつ引いて，小数が完成したときに数の大きいほうが勝ち。
【資料１４】数が大きいほうが勝ちゲーム ルール
ゲームを何度かやるうちに，相手に9が出た時点で，「負けた。」と呟く児童Gの姿が見られた。
ここで，【資料１５】のようにゲームの経過を取り上げ，「どうして，9が出るとGさんは負けと言ったでしょう？」と尋ねた。
抽出児Aは「だって空いているところに0～8，何が入っても勝てないよ。9が出たら勝負は終わりじゃん。」と答えた。
他の児童も納得したので，「9を1/10の位に入れれば勝つんだね。」と価値付けた。
ここで，「じゃあ，ルールをどう変えればいいかな？」と尋ねたところ，「0～9の山札を2つにすればいい。」という児童Gの言葉から，ルールを変え，ゲームに取り組ませた。
十分に取り組ませたところで，「勝つコツは分かった？」と尋ねた。
そうしたところ，児童Fは「さっきと一緒で，9や8を1/10の位に入れれば勝てるよ。」と話した。
「なぜ，1/10の位に9や8を入れると，大きな数ができるか」に迫ろうと，「【資料１５】では，確かに1/10の位では勝っているけど，1/100,1/1000では数字負けているじゃん。なんで1/10の位だけに注目すれば，数比べができるの？」と問い直した。
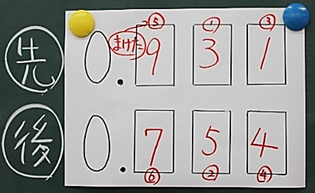【資料１５】児童Gのグループのゲームの経過児童たちは悩み，教室に掲示されている授業のまとめを見ていた。この時，抽出児Aは，理由までは考えをもつことができなかった。
児童Dが，「あの写真（【資料８】）といっしょだ。」と呟いた。そこで児童Dを指名すると，「今回も0.001にしてみると，0.001が754個と931個。こうすれば比べられるでしょ。」と発言した。
児童Dの発言の付け足しで，抽出児Aも「0.001にすると同じだから比べられる。」と発言した。
模造紙を貼り，いつでも既習事項を見直せるようにしたことで，主体的に考え，0.001に直す考えを抽出児Aはもつことができた。
また，自分たちで，既習事項を使って，本時の学びを深めている姿が見られた。手立てⅠ－②は有効に働いたといえる。
小数のたし算・ひき算（第７・８時）
なぜ，筆算のとき，位をそろえなければならないの？【手だてⅡ―②】
「5.17＋4.51」を取り扱った。
ここでは，「同じ位同士を足して，5＋4＝9，1＋5＝6，7＋1＝8。だから9.68だよ」や「いつも通り，筆算でできたよ。」と全児童が答えにたどり着くことができた。
筆算のやり方を確認した後，「7＋3.51を筆算で計算してみよう。」と問題を伝えた。
これも，全員が位を揃えて筆算を書き，10.51と筆算で答えられた。
ここで，なぜ位をそろえなければいけないかを児童に追究してほしかったので，「先生が前にいた学校で【資料１６】のように書いた子がいたんだけれど，どう？」と提示した。
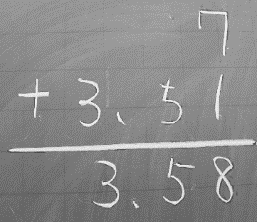【資料１６】担任の誤答の提示児童たちはすぐ，「7はもっと左だよ！一の位。【資料１７】」と話した。
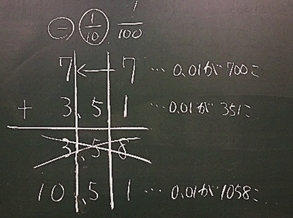【資料１７】誤答の再検討そこで「なんで，一の位に書かんといかんの？」と尋ねた。
「7は0.01が700個，3.51は0.01が351個。合わせると，0.01が1051個で10.51。」【資料１８下線部】，「前，Bさんが言ってくれたけど，位が違うと，マグネット１つの数の意味が変わってくるから，だめだよ。同じ位にそろえて足さなきゃ。」【資料１８点線部】と，担任の考えはなぜ違うのか，抽出児Aの発言を言い直しながら，対話的に検討し，学びを深めている。手立てⅡ－②は有効に働いた。
抽出児A：だって，７は１の位の数字だよ。1の位に入らないとおかしい。
T：Bさん，付け足しあるの？
児童B：Aさんに付け足しで，7は0.01が700個，3.51は0.01が351個。合わせると，0.01が1051個で10.51。先生のはおかしい。【資料１７】
T：Dさん，まだ手を上げているね。Dさんの言葉で，2人の話をまとめてくれるかな。
児童D：位取り板で見ても，先生のやり方だと，1の位の7つのマグネットを，1/100の位のマグネットと足しているでしょ。前，Bさんが言ってくれたけど，位が違うと，マグネット１つの数の意味が変わってくるから，だめだよ。同じ位にそろえて足さなきゃ。
【資料１８】誤答の再検討での対話
研究の成果と課題
仮説Ⅰの成果
「既習事項とのずれ」を意識できるように，既習の問題と，新しい問題を提示したことは，第１時【資料４】から分かるように，課題を具体化する上で有効に働いた。
また，既習を振り返ることがえきるように，学習の足跡を掲示したことは，第４時の児童たちが【資料９，１０】を見て，主体的に問題を解く姿から有効に働いた。
手だて①，②を講じたことは児童が主体的に学び，深い学びを導くために，有効に働くことが分かった。
仮説Ⅱの成果
第１時【資料５】や，第４時の終盤での話し合いのように，友達の話を自分の言葉を言い直すことで，抽出児Aはもちろん，まわりの児童の考えも深まる姿があった。
また誤答をあえて提示したことは，第６時【資料１５】，第７・８時【資料１８】のように，児童たちが正答は何か考える中で，対話的に深い学びをしていることが分かる。
手立て①，②は有効に働くことが分かった。
今後の課題
手だてⅡ－①「友達の意見を自分の言葉で言い直す」ことは，【資料４】のように問題解決へのとっかかりにはなったが，児童たちに，「本時の課題は何だったか。」と尋ねると，全ての児童が同じ課題を意識していたかは検証できなかった。
児童たちなりの言葉で，課題を言語化する場を持てば，児童は同じ課題を意識して学習に取り組め，より首尾一貫した議論になったと考える。そうすれば，対話の場面でも，さらに活発な議論になるだろう。
また，【資料１８】のように，抽出児Aや児童B，Dは学習をたしかに理解できているように読み取れるが，この気付きは，他の問題でも適用できると考えているのか，それとも，この問題だけしか適用できないと思っているのか，各児童の到達度を検証できなかった。
まとめも児童の言葉で言い直しをすれば，クラス全体の学習の到達度も高まると考える。この２つの場面で言い直しを手だてとして取り入れ，児童の思考をより表面化させながら来年度の実践を進めたい。
関連記事
コメント