中学校2年生から変化の割合を習うのですが、あれは、数学的にどんな意味があるのでしょう。
特に2年生では、一次関数で変化の割合を勉強するため、(傾き)=(変化の割合)となり、覚えましょうと話して終わってしまうことも多いと思います。
本当は、中3の二次関数のように、増加量が一定にならない場合になって初めて必要性が出てくるというものだと思います。
そして、高校の微分まで睨んで勉強をつなげていきたいところですね。
今日は、中高の学習がつながるようの授業を考えてみました。
変化の割合と微分の定義(教材研究)
変化の割合の公式は
$(変化の割合)=(yの増加量)/(xの増加量)$
です。
一方、微分の定義は
$$ f'(a)= \lim_{h \to 0} \dfrac{f(a+h)-f(a)}{h}$$
です。
変化の割合の式をよく見ると、xの増加量を限りなく0に近づければ微分をしたことと同じことになることがわかります。
例を挙げて考えてみましょう。
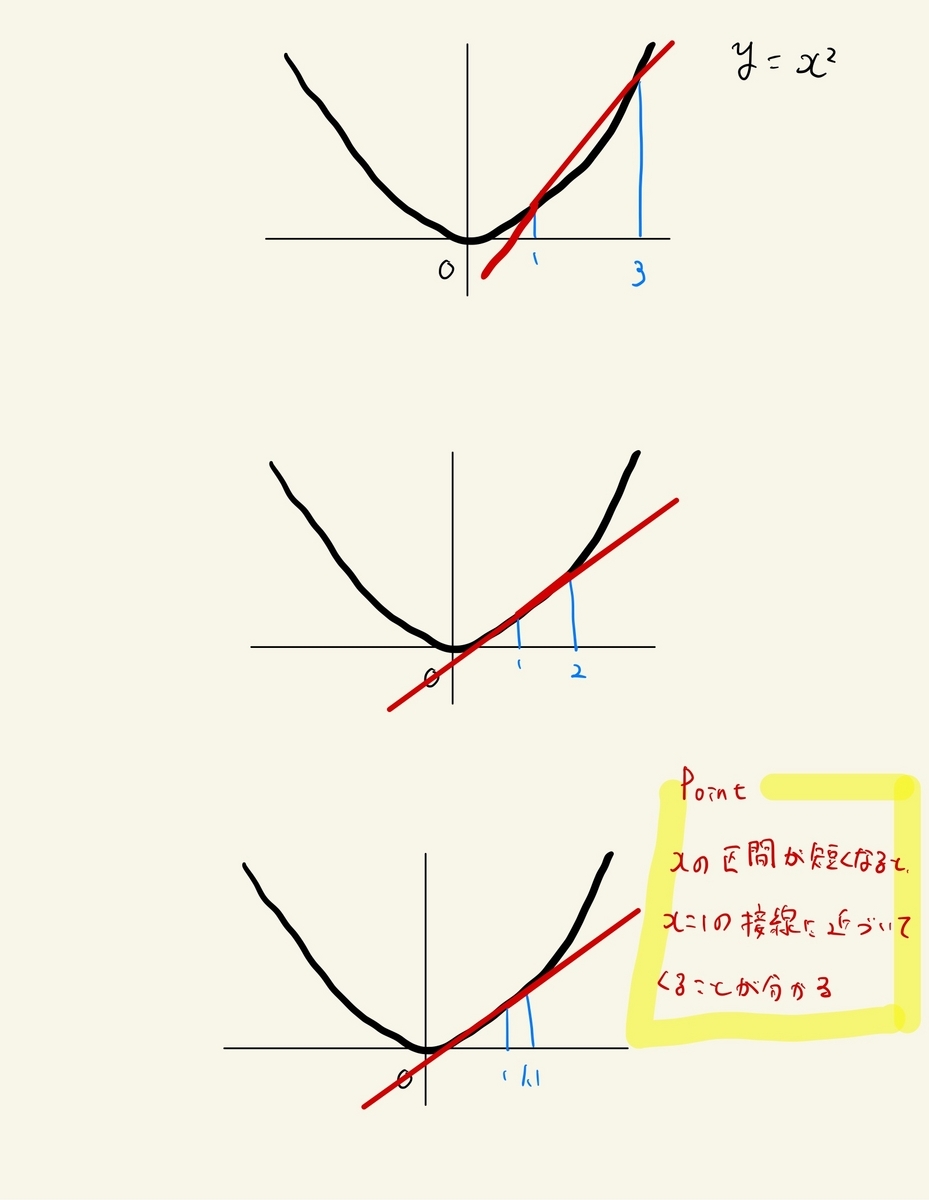
$f(x)=x^2(y=x^2)$において
$x$が$1$から$3$の間の変化の割合を考えてみます。
変化の割合の定義式から、
$変化の割合= \dfrac{9−1}{2}=4$となります。
では、$x$が$1$から$2$の間の変化の割合は
$変化の割合= \dfrac{4−1}{1}=3$
さらに$x$の区間を短くして、$x$が$1$から$1.1$の変化の割合は
$変化の割合= \dfrac{1.21−1}{0.1}=2.1$
もっと$x$の区間を短くして、$x$が$1$から$1.01$の変化の割合は
$変化の割合=\dfrac{1.0201−1}{0.01}=2.01$
ほら、$f′(1)=2$に近づいてくることがわかりますね。
微分で生徒が躓く理由は、
— のらりくらりteacher (@math_investment) February 18, 2023
・序盤に平均変化率(変化の割合)、微分係数、導関数などのよく分からない用語が怒涛の勢いで登場する
・かと思えば公式を覚えさせられ、あとはこれ使えばOKとされる
→「結局微分ってなんなんだ」となる
用語、計算は一旦置いといて、とにかくここに立ち返らせたい pic.twitter.com/Zf4pIO4px2
斜面を転がるボールを使って(中学知識まで)
$y=x^2$
の関数は、斜面をボールが転がる時の、ボールが転がる時間と移動距離の関係を表すのに使われることが知られています。
教科書と同じようにここは説明した後、子どもに以下のように発問します。
「さて、ボールが転がりはじめてから、3秒たった時、ボールの速さは幾つでしょうか?」
皆さんはどうやって答えますか?
反応例として
- 2秒から、3秒の平均の速さで求める子ども→秒速5m
- 3秒から4秒の平均の速さで求める子ども→秒速7m
と2つの考えが出てきます。
ここで、2つの出てきた数字だけを紹介し、
「同じ3秒の時の速さを求めたのに、なんで数字が変わってくるんだろう。もちろんどちらも正解だよ。」
と問い返します。
そうすると、子どもは計算に使った秒数が違うことに気づきます。
そこで、変化の割合の式を思い出させ、
「みんなのやったことは二次関数の変化の割合を求めたんだよ。一次関数では変化の割合は一定(傾きと等しい)のに、なんで違ってきたの?」
とさらに問い返します。
子どもは二次関数の曲線に目をつけ説明をするでしょう。
ここまで来れば、
二次関数において
- 変化の割合は一定ではないこと
- 変化の割合が一定にならないのは曲線だから
ということをおさえることができます。
ここで、中学校の変化の割合の学習は終わりでいいのですが、せっかくなので高校レベルまで1つ突っ込んでみましょう。
ねらいは、「微分の感覚を掴ませる」です。
どう発問しますか?
斜面を転がるボール(微分の導入まで突っ込んで)
「さっきはどちらも正解といったけれど、できれば2つの答えの隔たりを少なくしたい。
ボールが転がり始めてから3秒後の瞬間の速さを求めるにはどうする?」
と聞きます。
きっと、3秒から3.1秒や2.9秒から3秒の間を計算する子どもがでてきます。 そこで同じように比べれば、誤差は少なくなります。
そこまで分かれば、3秒から3.01秒の間の速さを調べる子も出てくるでしょう。
そうやって、測定区間を短くすればするほど、瞬間の速さに近づくことに気づかせます。
今回なら秒速6mに近づいてきます。
そこまで来たら、
「実は、高校2年生ではこの瞬間の速さを見つける方法を勉強するんだよ。
微分っていうんだ。
難しい数式が出てくるけれど、みんながやったように、測定区間を短くすれば、瞬間の速さが求まるよってことを勉強するんだ。
しかも、みんな小数を使って何度も計算して、秒速6mに近づくことを見つけてくれたけど、暗算で求められるようになります。
どんな秘密があるかな。
見つけてみてね。」
と授業を終えます。
やりたい子は、ボールが1秒後、2秒後の瞬間の速さの収束値を求め、
導関数$y=2x$を見つけ出すことでしょう。
この段階では何か秘密がありそうと思わせれればそれで良いと思います。
まとめ
二次関数の変化の割合のポイントは
- 変化の割合は一定ではないこと
に気づかせることです。
更には、
- xの区間を短くすると、どんなことが起こるか
に注目させることで、高校への学習の接続が出来ると思います。
よく中高の接続教材として、確率がよく取り上げられますが、関数でも出来そうです。
いかがでしょうか?




コメント