今回は、「平行線と面積」の学習で教材研究したことをブログに残します。
実は授業をやっていて、なんでここで、この勉強をするのかな。深まりがあまりない分野だなと思っていました。
そこで、しっかり教材研究してみようと思ってやりました。がっつり。教材研究。
高校の先生にも話をして授業も見てもらったら、思わぬ発展形があることがわかりました。
「平行線と面積」 教科書での説明
教科書では、以下のような説明がなされています。
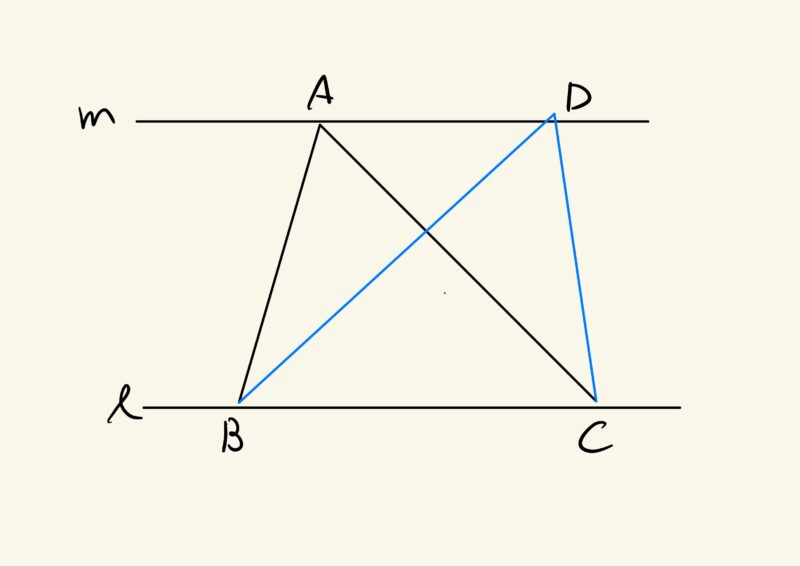
$l$//$m$ のとき、辺 BC を底辺とする2つの三角形 △ABC と △DBC は高さが等しくなるので、面積が等しい。
即ち $l$//$m$ ならば △ABC=△DBC である。
また、これの逆も成り立つ。△ABC=△DBC ならば $l$//$m$ である。
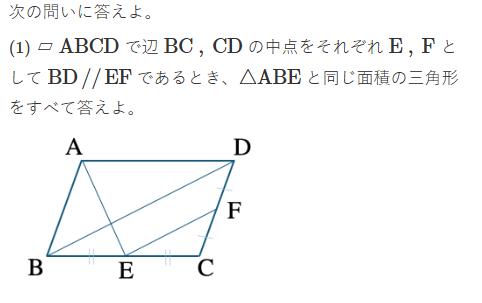
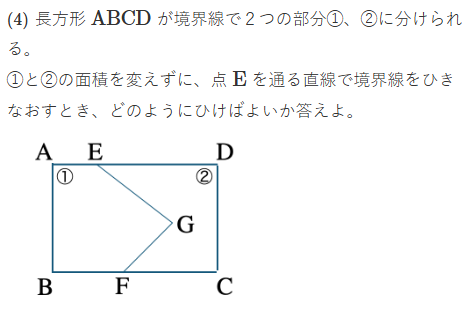
そして、これを使って、啓林館の教科書では、以下のような系統の練習問題を解いていきます。
この学習は今後どの分野につながっていくかのでしょうか。
- 円周角の定理(図形の見方)
- 入試問題の出題
- 指導要領を超えて、発展内容として(3次元への拡張)
この3つの切り口で今回はお話したいと思います。
「平行線と面積」と「円周角の定理」(図形の見方)
平行線と面積の部分と、円周角の定理。
「共通な底辺・弧から、にゅっと2本線が出ていれば、面積・角が同じになる」ことが、共通しています。
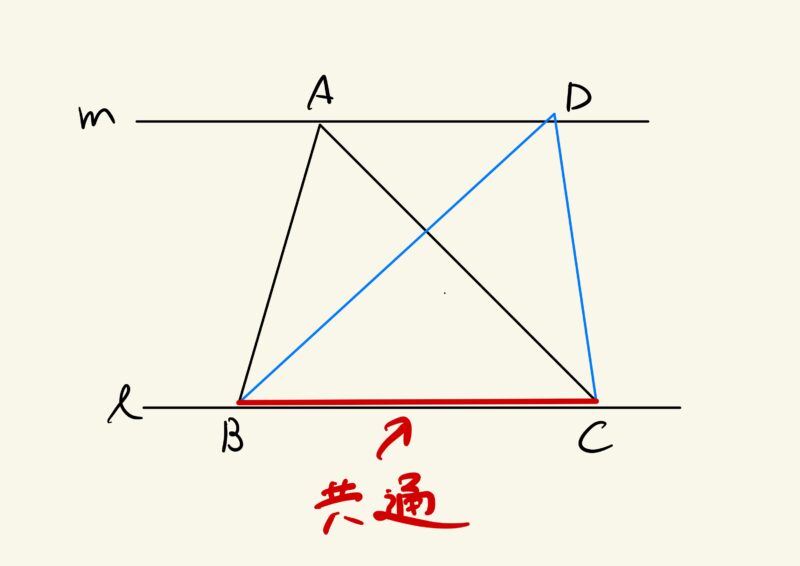
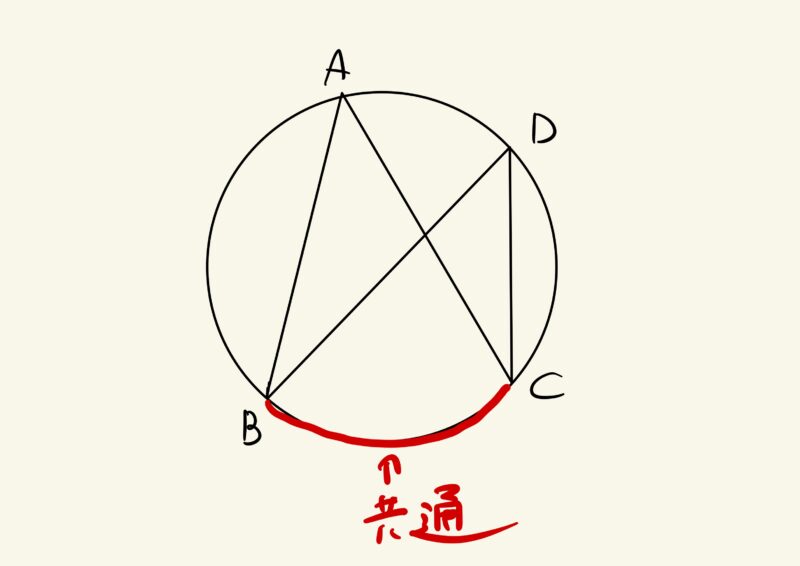
案外等しい面積や等しい角を見つけることは、結構子どもはすぐ見られるようになりません。
2年生で、共通の辺から出ているものを見つけられるようになると、円周角の定理も、楽になるのではないかと思います。
入試問題と「平行線と面積」
実際に、底辺が共通で、同じ高さの三角形の面積を見ていくことは、入試問題では見たことがありません。
この知識を応用して、「面積比」の問題を出しているのではないのかなと思います。
例えば以下のような問題です。
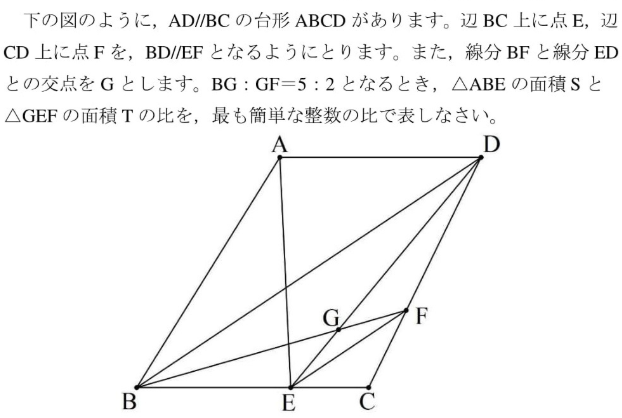
ー2021年度 広島県公立高校入試 大問3
△BEFで、BG:GF=5:2なので、△BRG:△FEG=5:2と面積の比が求まります。
これは、高さは共通なので、底辺の長さの比で、面積の比が決まるのです。
これは、「平行線と面積」の学習を応用しています。
この系統の問題は、入試でも解ける生徒は少ないです。差の出やすい分野です。
【発展】平行線と体積
中学校では取り扱いませんが、「平行線と面積」の2次元の話から、3次元へと拡張も可能です。
以下のことが言えます。
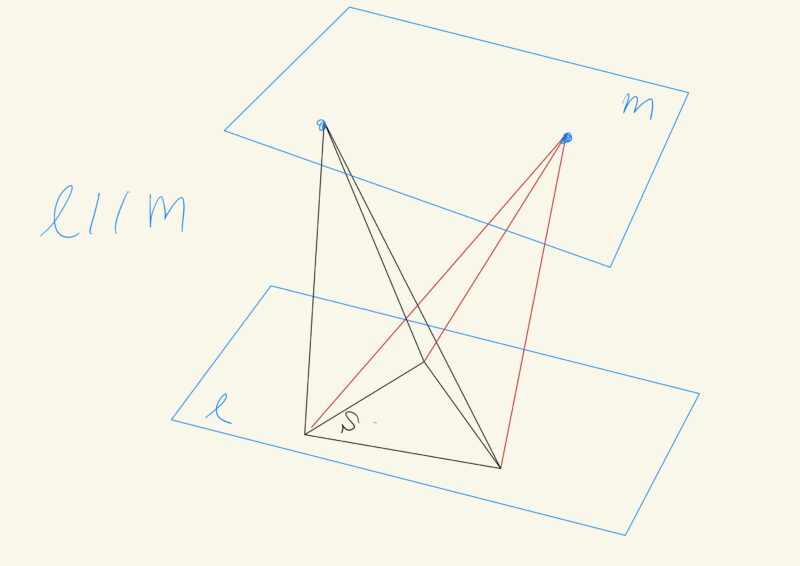
面$l$//面$m$ のとき、面Sを底面とする2つの立体AとBは高さが等しくなるので、体積が等しい。
即ち 面$l$//面$m$ ならば 立体A=立体B である。
また、これの逆も成り立つ。立体A=立体B ならば 面$l$//面$m$ である。
「平行線と面積」を「平行面と体積」にまで拡張しました。
上記のことは、中2の学習を応用すれば、正しいと簡単に理解できます。
最後に

今回は「平行線と面積」をテーマに教材研究をしてみました。
教科書で紹介されている定理は、当たり前といえば当たり前なので、さらっと流せそうですが、子どもは案外理解できていません。
意外と奥が深い分野です。
こうやって立ち止まって教材研究すると新たなことが見えてくるとともに、色んな人と話題にしていくと、さらに教材研究が深まる楽しい分野でした。
みなさんはいかがでしょうか?ぜひ気づいたことをコメントください!

参考HP






コメント