連立方程式では、加減法でも、代入法でも、とにかく「一つの文字を消去」して、一次方程式に帰着するのが大切になってきます。
代入法だと置き換えなのでイメージがつきやすかったり、生徒から意見が出てきたりするのですが、2つの式同士を引いて、文字をひとつにするという方法は、中学生にとって目新しいアイデアとなります。
そこで、そのイメージをつくるために、こんな図をかいて理解を促しています。
連立方程式の別の授業についてはこちらをご覧ください!
加減法の導入
例えば、以下のような連立方程式があったとします。
$$\begin{eqnarray} x+y&=&4 \\ x+2y&=&10 \end{eqnarray}$$
このときに、以下のような図をかきます。
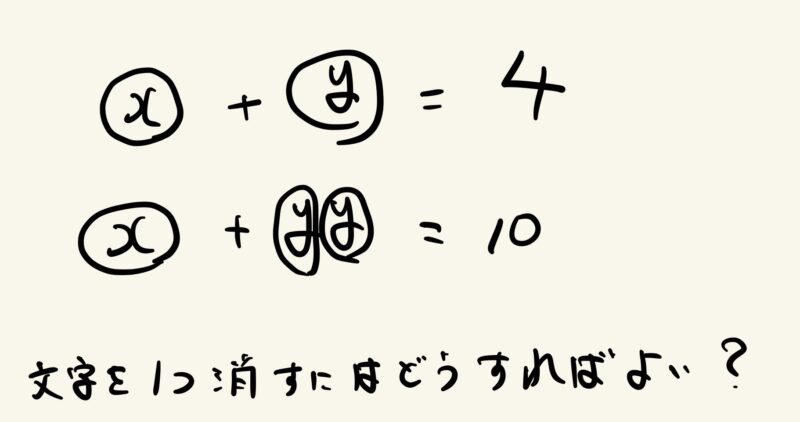
式をビジュアル化することで、「xの数が揃っているから上から下の式を引けばよい」というイメージがわきやすくなります。
係数だと、最初つかめない子どもも多いのですが、こんな形にすると、子どもが取っかかりやすくなります。
教科書だと、鉛筆とノートの絵で説明しているものもありましたが、書くのも手間ですし、抽象化してもよいのかなと思っています。
片方の式を○倍して係数を揃える問題
次は、片方の式を○倍して、係数をそろえるパターンに入ります。
$$\begin{eqnarray} 2x+3y&=&4 \\ x+2y&=&10 \end{eqnarray}$$
その場合も、まずは図に書いて、単純に2つの式を差し引きするだけでは計算できないことを確認しましょう。
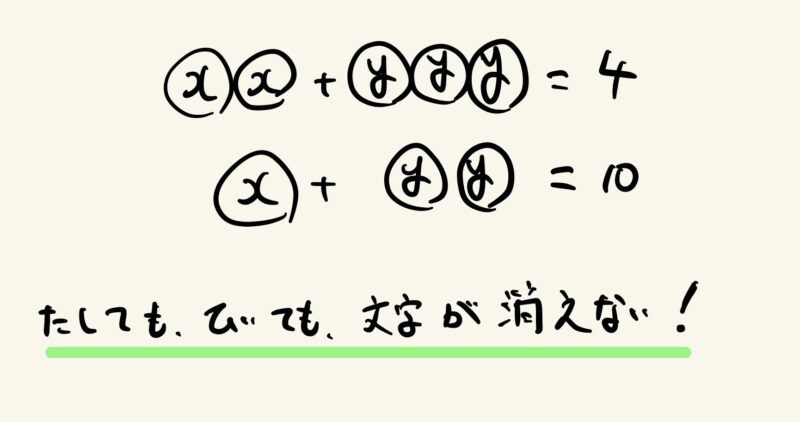
子どもからは「xの数が揃うといいのにな」ときっと声が出てきます。
その時に、「じゃぁ下の式を何倍すればxの数がそろう?」と水を向けていきます。
「2倍していいの?」と子どもは言うかもしれません。
そういう子どもはぜひ大切にしたいですね。
これは、一次方程式の学習でおこなった「等式の性質」を使っているから、大丈夫なのです。
そうやって、準備を整えていきます。
ここまでこれば、2つの式を○倍、△倍して係数を揃えるのもすぐわかりますね。
練習問題をこなしたい
連立方程式の分野は答えにたどり着くまでの過程が長いので、子どもによっては30分かけて2問しか解けないという子どもも出てきます。
私は、最初の1時間目は、「書き方を説明して書けるようになること」
係数をかけて合わせる問題がでてきたら、「係数を揃えて、差し引きをして、文字を一つにするところまで」でOKにする。
係数が分数や小数になった場合も同じで、文字を一つにした時点でOKにする。
というふうに省略をしています。
文字を一つにできたらもう子どもたちは解けると思うので、そこまでいったら、家庭で勉強すればよいと思っています。
まとめ
連立方程式の解を求めるようにするために、
- 文字式をビジュアル化しよう
- 連立方程式が複雑になってきたら、文字を一つにできたらとりあえずOK
後は家庭学習で!
ということを意識してやってみてはいかがでしょうか?
またご意見をください。






コメント