【中２ 図形 証明 指導案】証明途中で結論の内容を書いてしまう生徒への例え話

今回は、図形の証明について扱います。

色々約束事が多く、生徒が嫌になってしまいやすい単元ですが、できる限りシンプルにして、生徒に届くようにしています。

今回は、結論を証明過程に使ってしまう生徒の誤答についてどう直していけばいいかについて考えました。

生徒の誤答

証明の最初の授業で、以下の問題を取り扱いました。

ー啓林館．「未来へ広がる数学2」P112～113

補助線としてACを結んで、△ABCと△ADCの合同を示せば、角ABC＝角ADCを示せることは、多くの生徒がすぐ思いつきました。

ただ、その中で、次のように説明する生徒が多く見られました。

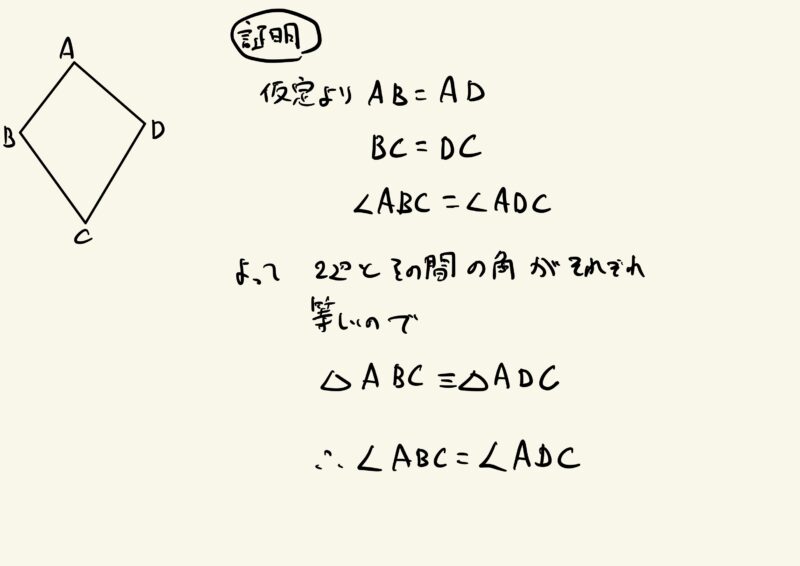
どこが間違いかわかりますか？

そうです、結論の角ABD＝角ADCの部分を証明過程で使っています。

典型的な誤答ですね。

ただ、なぜこれではいけないかのを説明しようとすると難しいですね。

そこで、自分はこんな例え話をしています。

コナンくんは、犯人は最後まで言わない

こんな時は、コナンくんを例に私は話をします。

「コナンくんは、犯人をAさんだということをみんなに説明したい。

どう説明するだろうか。

証拠を一つ一つ提示して、言い逃れができなくなったところで、最後に『犯人はAさんです！』と結論を言うでしょう？

ただ、証拠を提示している段階で『犯人はAさんです』ということを持ち出したら、おかしなことになるよね。

数学の証明も同じです。結論の部分は「犯人」の部分です。だから、使っていいのは、証明の最後だけ。

証明途中の部分では、決して結論の話を持ち出してはいけません。」

こんな話をすると、そりゃそうだと生徒は納得をしてくれます。

授業のまとめ

証明の細かい書き方は、次の時間にするとして、中学校で行う証明は、ざっくり以下の3つのプロセスを辿ることを伝えます。

これだけ整理をしておけば、結構次の時間、証明を細かくやっていっても、生徒はついていきます。

最後に

今日は、中学校2年生の合同の導入について記事にしました。

証明は、プロセスが長く、生徒は嫌になってしまいがちなところですが、重要なところ押さえておけば、実はそれほど難しい単元ではないと思っています。

生徒の誤答を上手に活用しながら、うまく言葉を組み合わせて、図形の証明をできるようにしたいですね。