連立方程式の問題を見た時に、子どもはどう反応するのでしょうか。
図を使ったり、1次方程式に帰着したりとエレガントな解法があったので紹介をします。
導入部分で、これだけいろんな解答が出てくると、ついつい楽しくなってしまいますね。
導入の時間のイメージにつながったら幸いです。
⇓次時の授業の記事はこちら!⇓
問題
36人で班を作ります
3人班と4人班を作ります。
「合計で10個、班を作りなさい。」と先生に言われました。
人が余ってはいけません。
3人班と4人班はそれぞれいくつできますか?
『未来へ広がる数学2』.啓林館.2018
さて、子どもたちはどんな解法をしたでしょうか?
解答
教科書にある模範解答
表にして、両方のグループの人数が、整数かつ合わせて10になるところを見つけています。
これは教科書にも書いてありますし、表出しやすい考えですよね。
こちらは割愛します。
図を使って
どちらかというと数学が苦手なある生徒が、こんな図をノートに書いていました。
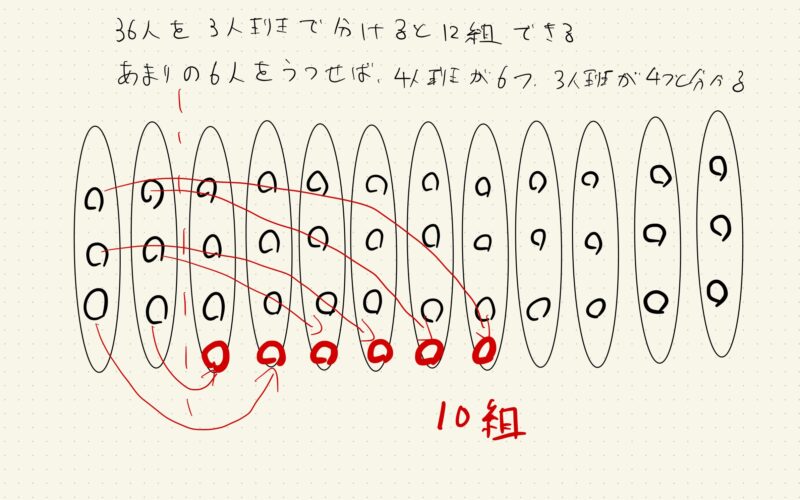
皆さんは、この解答どう思いますか?
解が分数でなければ、どんな時でも通用しそうな考え方ですよね。
これ、エレガントな解答だなと思いました。
2つの文字をつかって(連立方程式を立式)・1次方程式で解答

2つ同時に紹介します。
画像左の$3x+4y=36$とだけ書いた子がいました。
「なんで解けないの?」と全体に尋ねると
「文字が2つあって解けない」ことを確認しました。
また、子どもの中には、$x+y=10$の式も見つけていた生徒もいたので紹介して、
「文字が2つ、式も2つ。そうなると解けるようになります。それが今回の勉強、連立方程式と言います。」
と伝えました。
また、$3x+4y=36$だけを提示した時に、
「2つ文字があって解けないなら、1つの文字で方程式を表せばいいのでは?(画像右)」
と一次方程式でもう解答を導いた子どもがいたので、連立方程式の話をした後、一次方程式を提示しました。
そして、
「連立方程式と、1次方程式ってつながる所ないかな?」
と話して授業を終えています。
教科書では、加減法から進んでいますが、この子どもの意見を使って代入法から勉強を開始しようと考えています。
まとめ
いかがだったでしょうか。
生徒にビジュアルでわかりやすく、エレガントな図から、1年の学習ともつながりそうないいアイデアまで出てきました。
ただ、図を使った解答は私ではなくT2では入ってくださる先生が見つけて拾い上げてくれました。
T2の先生に感謝すると共に、僕1人では掬えなかった解答です。
T2のありがたさと、教材研究不足を感じました。
皆さんの授業の様子、ぜひ教えてください!






コメント