既知数を$a,b,c$で未知数を$x,y,z$で表すことを決めたのは誰でしょう?
じゃぁ、文字の式の乗法の”×(かける)”を書かないと決めたのは?
これって教科書には書いていませんよね。
授業でちょっとここらへんに触れるようにしています。
ちょうど、哲学の本を読んでいたら、そこら辺の説明が出てきました。
数学と哲学は密接な関係があるんだなと思って、ちょっとメモとして残しておきたいと思います。
皆さんは御存知でしたか?
文字式の表し方を決めたのはライプニッツ

ライプニッツは数学で有名ですが、哲学の世界でも賢人です。
というか、当時の学者は、自然科学から、哲学、神学まで何でも考えていたんですね。
ぜひWikipediaを見てください。すごいですよ。
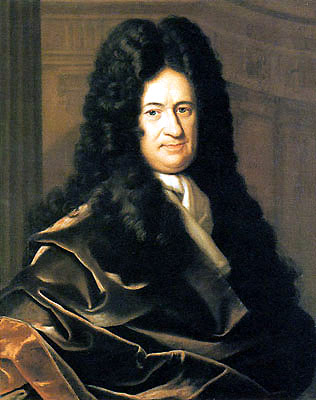
この人が、中学校1年生で勉強する「文字の式の表し方」を決めました。
文字式の表し方
- ×(かける)の記号は省略する
- 文字はアルファベット順に並べ替える
- 数⇒文字の順に書く
- 1は省略する
- 同じ文字の積は、累乗の形にする
- かっこの式と数との積では、かっこの前に数を書く
- 割り算は分数の形にする
- 分子全体にかっこがつくときは、かっこを省略
- 足し算と引き算の+、-は省略しない
これを生徒に提示すると、生徒からはいつも総スカンを喰らいます。
そこで、「ライプニッツという偉い人が決めたのだ!」と業績をいうと、子どもがひれ伏します(ホントかよ、権威を傘にする悪い教師である)
そうやって、ちょっとでも親しみを持ってもらうようにしています。
既知数をa,b,c 未知数をx,y,zと決めたのは「デカルト」
既知数をa,b,c 未知数をx,y,zと決めたには「デカルト」です。

怪人Xのように、分からない物をxと表すようになったのもここからと言われています。
教科書では、既知数、未知数の文字の使い方の説明はないので、デカルトを引き合いに出しながら、子どもに説明するようにしています。
「我思う、ゆえに我あり」
この名言を言った人だよ!というと子どもも聞いたことがある!と言ってくれます。
「x」の諸説
Wikipediaの二次方程式に項にも「x」の記述を見つけました。
アッバース朝時代に活躍した中世イスラムの数学者フワーリズミーは二次方程式に2つの解があることを発見した。
フワーリズミーの著作『インドの数に関して、アル=フワーリズミー』(ラテン語訳『アルゴリトミ・デ・ヌーメロ・インドルム (Algoritmi de numero Indorum)』)はラテン語に翻訳され、ヨーロッパに伝わった。
フワーリズミーは二次方程式における未知数を「shay’」(シャイ=とあるもの)という言葉で表現したが、フワーリズミーの著作がヨーロッパに伝えられる段階で、「x」を「sh(シ)」と読むポルトガル語を通過する際に、shay’の「sh」が「x」に置き換えられたといわれる。
未知なるものを「x」と呼ぶことには、このような背景があるとされる-wikipedia「二次方程式」
これもデカルトが関係しているのでしょうか?
発音由来で、xが決まったんですね。
最後に

数学も、数学として独立してるのではなく、他の学問とも密接して関係しているんだよと伝えたいなと思っています。
数学では、あまり他の学問との関連は喋りませんが、こんなふうに教師としても知っておく、機会があれば伝えることで、子どもの興味が持ちやすくなるのではないかなと考えています。
みなさんもぜひ話してみませんか?

数学小話はこちらの記事でも紹介しています。
文字式の部分の授業も紹介しています。
参考文献・参考HP
参考文献
参考HP
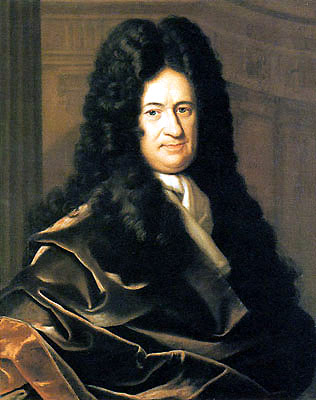
ライプニッツのイラスト

デカルトのイラスト









コメント