中学校から本格的に始まる文字。
小学校では、□で表していたのに、中学校に入ると突然文字を使い出します。
中1の生徒からは毎年非難轟々です。
なんでわざわざ文字で表すんだ!と怒られます。
けれど、やっぱり文字は便利なのです。
便利だから使われるのです。
今回は文字式の歴史と、教科書で紹介されている問題を使って文字式の威力を実感できる場面を紹介します。
文字式の歴史

古くはローマ時代から
数学の文字式が登場したのは、それほど古いことではありません。
文献として残されている一番古いものには、3世紀、アレキサンドリアで活躍したとされているディオファントスの「数論」だそうです。
この本では、方程式が文字を使って表されています。
しかしながらディオファントスの文字式は、それ以降使われることはありませんでした。
5世紀のインド
次に歴史に現れるのは、5世紀のインドのブラーマグプタです。
彼は色の名前を使って未知数を表し、連立方程式をときました。
彼の文字式は12世紀のバースカラに引き継がれて使われましたが、インドではその後大きな発展はなかったようです。
本格的に使われたのはフランスの「ビエト」から
今の数式のようなかたちで文字を本格的に使ったのは「代数学の父」と言われる16世紀のフランスの数学者ビエト(1540~1603)です。
ただ、ビエトもまた、ギリシア時代からの、$a$を線分の長さとすると、$a^2$は面積、$a^3$は体積であるから、$a^3×a^2$は意味を持たないという考えから脱却できませんでした。
つまり、実生活の中だけの数学に囚われ、生活の中で表せないものは意味がないと考えていたわけです(実際に$a^5$は生活では意味をもちませんね)
これを断ち切った人が、同じくフランス生まれの哲学者デカルト(1596~1650)です。
彼は、単位の長さ1と比例を導入することで、何乗の量でも直線上の長さとして表す事ができるとしました。
数を面積や体積などの数量から一旦切り離すことは、数学の計り知れない発展につながっていきます。
日本では
日本では、関孝和(1642?~1708)が方程式の変数を文字で表す点鼠術を開発しました。
関孝和は、1674年にこの点鼠術を「発算算法」に著し、その後の和算の高度な発展に貢献しました。
この他にも微分・積分や円周率の計算法などに力を入れていました。
微分・積分に関しては、イギリスのニュートンやドイツのライプニッツとほぼ同時期に、その確立の一歩手前まで来ていたとも言われています。
なんで文字式は便利なの?
さて、ここから本題です。
中学1年生が苦しむ、文字式。
なんで数学では文字が重用されるのでしょうか?
中1の教科書から
以前の啓林館の教科書にはこんな問題が載っていました(記憶の中ですが)
地球を完全な球として赤道の地上1mのところに電線を張りたいと思います。
この電線の長さは、地球の周囲よりも何m長くなるでしょうか?
但し円周率はπとします。
地球の半径は与えられていないので、計算しようとすると困ってしまいます。
けれど、これを文字で表してみましょう。
地球の半径をrとします。
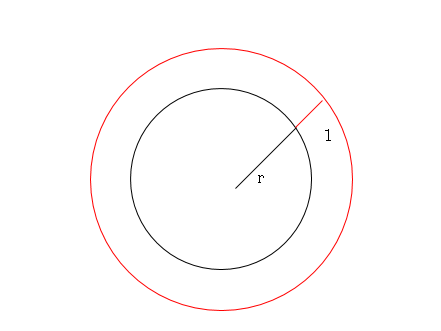
地球の円周は、2πrと表すことができます。
電線の長さは、半径r+1の円周ですから 2π(r+1)となります。
ここから、(電線の長さ)ー(地球の円周)を計算すると、
2π(r+1)ー2π=2πr+2πー2π=2π と出ます。
実際の値は、2×3.14(π)=6.28mほど長くなればいいわけです。
r(地球の半径)が計算の中で消えてしまい、地球の長さが幾つかわからなくても解くことができるようになりました。
これは、地球だけでなく、木星、月、ゴルフボールやサッカーボールでも同じ結果になります。
同じ結果になるのが文字式のすごいところです。
ボールでも惑星でも一緒と、「抽象化」をすることができるのです。
中2 多角形の外角と内角
三角形の内角の和は180度です。
それが四角形、五角形となっていくと、内角の話はどうなるのでしょうか?
四角形は、対角線に切ることで、三角形が二つになります。
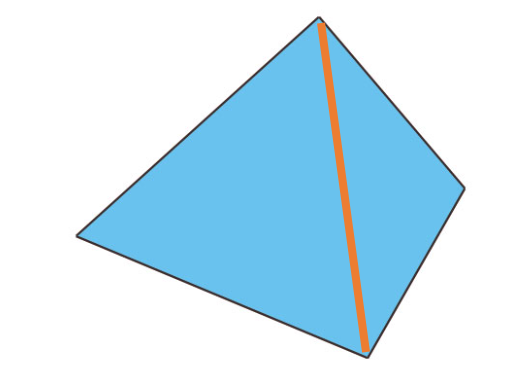
よって、内角の和は180度×2=360度となるわけです。
五角形も同様に1つの頂点から対角線を引いてみましょう。
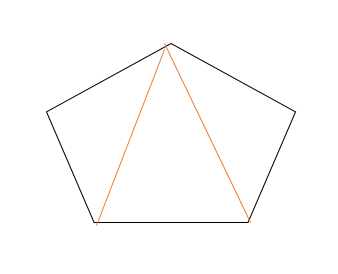
三角形が3つ出てきます。
よって五角形の内角の和は180度×3=540度となるわけです。
そうなってくると六角形、七角形、・・・百角形だったら、と数をどんどん増やしていきます。
一般にn角形は一つの頂点から引いた対角線によって(n-2)個の三角形に分けられるので、次のことが成り立ちます。
n角形の内角の和は、180度×(n-2)
この式があれば、nが100だろうが、1000だろうがその内角の和を求めることができます。
また、上記のように、まどろっこしい三角形の分割を行わなくても、式を覚えて置くだけで、どんな図形の内角の和もいくつか求めることができるわけです。
「一般化」することで、覚えることが少なくなりました。
コラム 本記事で出てくる数学者の逸話
ディオファントスってこんな人

アレクサンドリアのディオファントスは、古代エジプトのアレクサンドリアで活躍した数学者です。
生まれたのは紀元200年ごろ、亡くなったのはおそらく284年から298年ごろといわれています。
彼の生涯の詳しい記録はほとんど残っていませんが、その業績は後の数学に大きな影響を与え、「代数学の父」と呼ばれることもあります。
ディオファントスの代表的な著作は『算術(Arithmetica)』という本です。
もともとは13巻あったとされていますが、現在残っているのはギリシャ語の写本で6巻、アラビア語の写本で4巻だけです。この本の中で彼は、整数や有理数の解を求める問題を数多く扱いました。
たとえば「3つの数を平方数にして、和も平方数にせよ」といったような、今でいう“数論”の問題です。こうした方程式は、のちに「ディオファントス方程式」と呼ばれるようになりました。
また、『算術』の中には、ピタゴラスの定理に出てくるような a² + b² = c² の形を持つ「ピタゴラス数」を見つける一般的な方法も書かれています。
こうした考え方は、後のヨーロッパ数学の発展に深く影響を与えました。
ディオファントスには、ちょっと面白いエピソードもあります。
彼の墓碑には次のような文章が刻まれていたと伝えられています。
「彼の人生の6分の1は少年期、12分の1は青年期、その後7分の1が過ぎて結婚した。5年後に子どもが生まれたが、その子どもは父の人生の半分しか生きなかった。そして子どもが亡くれてから4年後に、彼もこの世を去った。」
この文章をもとに方程式を立ててみると、ディオファントスの寿命は84歳だとわかります。
まるで古代の数学者からの謎解きメッセージのようで、今でも数学の授業などで紹介されることがあります。
ディオファントスの考え方は、単に数字を扱うだけではなく、「未知の数を文字で表して考える」という代数学の基本を生み出しました。
私たちが今、x や y を使って方程式を解いているその原型が、すでに彼の中にあったのです。
現代数学の礎を築いたディオファントス。彼の残した数式や物語には、今もなお“数のロマン”が息づいています。
ビエトってこんな人
フランソワ・ビエトは、16世紀のフランスで活躍した数学者であり、法律家でもありました。
1540年にフランス西部のフォントネー=ル=コントで生まれ、1603年にパリで亡くなっています。
彼は「近代代数学の父」と呼ばれる人物のひとりで、今日の代数の考え方を形づくる重要な役割を果たしました。
ビエトの最大の功績は、「数を文字で表す」という発想を代数学に導入したことです。
彼以前の数学では、数字をそのまま扱う具体的な計算が中心でした。
しかしビエトは、未知の数や既知の数をそれぞれ文字で表し、記号を使って一般的な関係式として考える方法を確立しました。
これはまさに、現在の方程式の考え方につながる大きな転換点でした。
彼のアイデアは、のちのデカルトやフェルマーといった数学者たちに受け継がれ、現代の代数学の礎となっていきます。
たとえば、私たちが学校で習う「ビエトの公式(Vietaの公式)」――高校で習う、2次方程式の係数と解の関係を表すあの有名な公式――は、彼の名を冠したものです。
ビエトはまた、数学以外の分野でも活躍しました。
もともとは法律家として王に仕え、政治顧問として働いていましたが、同時に数学の研究にも情熱を注ぎました。
さらに彼は、敵国スペインの暗号通信を解読したことでも知られています。
実務の世界と学問の世界、その両方で力を発揮した人物だったのです。
彼の代数学は、単なる計算の道具ではなく、考え方そのものを整理し、抽象化するものでした。
数字を超えて「記号で表す数学」を生み出したことで、数学はより普遍的で強力な言語になりました。
もし彼がいなかったら、私たちは今でも「x」や「y」を使って式を書くことができなかったかもしれません。
フランソワ・ビエト――数字に文字の命を吹き込んだ、代数の時代を切り開いた人です。
デカルトってこんな人

ルネ・デカルトは、17世紀フランスの哲学者であり、数学者でもありました。
1596年にフランスのラエで生まれ、1650年にスウェーデンのストックホルムで亡くなりました。
彼は「近代哲学の父」と呼ばれ、また数学の世界でも「解析幾何学の創始者」として知られています。
デカルトは、「我思う、ゆえに我あり(Cogito, ergo sum)」という有名な言葉を残しました。
これは、「すべてを疑っても、疑っている自分の存在だけは確かだ」という考え方です。
彼はこの発想から、「確実な知識を築くためには、まず疑うことから始めよう」とする合理的な思考法を打ち立てました。
一方で、数学の分野でもデカルトの功績は非常に大きいものがあります。
彼は「代数」と「幾何」を結びつける考え方を生み出し、解析幾何学という新しい分野を開きました。
私たちが今、グラフや座標平面を使って関数を表すときの「x軸」「y軸」という考え方は、まさにデカルトの発想から生まれたものです。
彼の名前から、今でも「デカルト座標系(Cartesian coordinate system)」と呼ばれています。
また、哲学の世界では「心身二元論」を唱えました。
これは、人間を「思考する心」と「物質としての身体」という二つの側面から考える立場です。
この考えはその後の哲学や心理学にも大きな影響を与えました。
デカルトは、科学・哲学・数学のあらゆる領域に共通する「理性による理解」を重視した人でした。
彼の考え方は、「疑うことから始めて、自分の頭で考える」という探究の姿勢そのものです。
もしデカルトがいなければ、私たちは今のように数と図形を一緒に扱う数学を学ぶことも、「自分の考えをもとに真理を探す哲学」を持つこともできなかったかもしれません。
デカルトはまさに、思考する力の大切さを教えてくれる人物です。
こちらの記事でも、デカルトについて触れています。合わせてご覧ください。
関孝和

関孝和(せきたかかず)は、江戸時代前期の日本を代表する数学者であり、「算聖」とも呼ばれた人物です。日本独自の数学である「和算」を大きく発展させたことで知られています。
生まれた年ははっきりしていませんが、1637年または1642年ごろとされ、上野国藤岡(現在の群馬県藤岡市)出身と伝えられています。
武士の家に生まれ、のちに関家の養子となりました。甲府藩の勘定方を務めたのち、幕府の旗本としても働き、実務の傍ら数学の研究を続けました。1708年に亡くなりました。
関孝和の最大の功績は、方程式を解く新しい方法を日本独自に体系化したことです。
彼は「傍書法(ぼうしょほう)」と呼ばれる独自の代数記号法を考案し、複雑な数式を整理して解く道を開きました。
また、円周率や体積の計算、幾何学的な問題にも挑戦し、西洋の数学と比べても高い水準の成果を残しています。
さらに、彼の研究は弟子たちによって「関流(せきりゅう)」として受け継がれ、日本各地に広まりました。
和算は、寺社に奉納される「算額(さんがく)」などを通して庶民の間にも広がり、日本の数学文化の礎となりました。
関孝和は、武士でありながら数学に情熱を注ぎ、生涯を通して「考える数学」を探求した人でした。
彼の功績は、日本における数学の自立を象徴するものであり、今日の数学教育や科学の精神にも通じています。
Podcast「大人の近代史」でも関孝和について触れられていました。
合わせて聞くと面白いかもしれません!
最後に

文字式ってめんどくさいというのは、入学まもない中学1年生の口からよく出てきます。
でも、電線の問題のように「具体的な数がわからなくても解ける」ことや、多角形の内角の和のように、「一般化」できるのは、文字式のすごい強いところです。
そのためには、文字は「さまざまな数が入る入れ物」というイメージを子どもに持たせられるかが勝負だと思います。以下の記事でその手立てを紹介しているので御覧ください。
歴史も踏まえつつ、文字式のすごいところを子どもたちに教えていければいいですね。
皆さんはどんな授業をやっていますか?
ぜひコメントで教えてください。

文字式の授業について、記事をたくさんあげています。合わせてご覧ください。
参考文献・参考HP
参考文献
参考HP














コメント