円周率はいくつですか？
3.14と皆さんは答えていただけると思います。
もちろん、3.14のあと1592・・・と永遠に続いていきます。
さて、なぜ円周率は3.14くらいなのでしょうか？
今日はそこを考えていきましょう。
円周率のルール
円周率とは何かを確認してみましょう。
円周率は（π、パイ）とは「円周÷直径」です。
あれ？3.14ではないの？と思うかもしれませんが、円周率≒3.14は、上のルールから導き出せる具体的数値になります。
円周率とは
「円周率π＝円周÷直径」というルールのもとで、円周率の値は常に3.14159265・・・となる。
ここを、問題を解いていく上で、「円周率を3.14とする」と書いてあるから、ゴチャゴチャになるんですね。
円周率π＞３であることの証明
さて、円周率は永遠と終わらない無理数です。
しかし、円周率が３より大きいことは比較的かんたんに証明できます。
やり方は「円に内接する正六角形」を考えます。
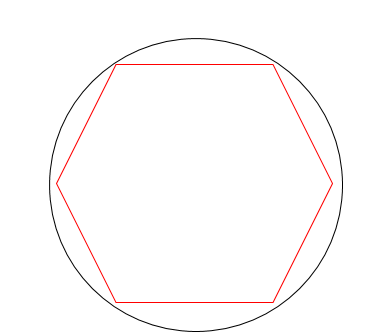
さて、ここに、中心と各頂点を結ぶ補助線を書き入れます。
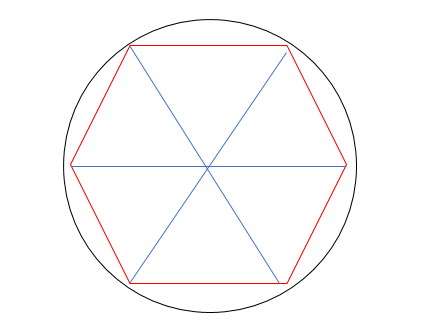
こうすると、一つの三角形は、頂角が６０度の二等辺三角形になりますね。
頂角が６０度ならば、底角も６０度。
つまり、それぞれの三角形は正三角形になります。
赤色１本分の線の長さは半径（青色１本分の長さ）と等しくなるので、
「正六角形の周の長さ」＝６×「円の半径」になります。
円の半径が２本分で直径になるので
「正六角形の周の長さ」＝３×「円の直径」
であることが導き出せました。
ところで、「円周率π」＝「円周」÷「円の直径」でした。
また、図より「円周」＞「正六角形の周の長さ」であることは自明です。
これらのことから、
ここから導き出せることが、
円周率＝「演習」÷「直径」
＞「正六角形の周の長さ」÷「直径」＝３
と証明できました。
以上より、円周率は３より大きいことが示せます。
東大の入試問題になったことも
ちなみにこれを応用して、「円周率＞３．０５であることを示す」ことは比較的簡単（高校レベル「三角関数」が必要ですが）にできます。
東京大学の入試問題に出題されたことがあります。
上記の解き方を見ながら皆さんも考えてみてはいかがでしょうか？
最後に
さて、ここからは余談ですが、ルール、ルールと言ってきましたが、数学では「定義」といいます。
「今から円の話をするんだけれど、円の話をするに当たって、円周率というのを決めます。
円周率＝円周÷直径とします。」と書くことが多いです（すごく砕けて書いていますが）
「します。」というのがポイントで、こちらで決めているんですね。
「円周率＝３」と定義すればいいじゃないかと思うかもしれません。
そうすると、厄介なことが起こります。
円周率は先程定義した通り、「円周÷直径」で「３．１４・・・・」と出てきます。
３と定義してしまうと、実際の生活の場（例えばタイヤを作るとか）で誤差が大きくなってしまいます。
また、数値で定義することで、色んな人の解釈で円周率の値が変わり、社会的にも問題が起こってしまうのです。
こういう不完全な定義をill-defindといったりします。
逆に「円周率＝円周÷直径」というように誰が読んでも１つに決まる定義をwell-defind（良定義）といいます。
今後の数学を成り立たせるうえで、混乱が起きないようにルール付をしているわけです。
そんな話をしていくと、また面白いかもしれませんね。
皆さんは円のところでどんな話をしていますか？是非コメントで教えて下さい。
数学小話でこんなことを話しても面白いのではと記事にしています。合わせてご覧ください！
参考文献・参考HP
参考文献
参考HP
コメント